これは面白い！ 論理クイズ傑作53問題まとめ【子供から大人まで】

史上最高に面白いクイズを集めました！！

クイズ好きが厳選した良問題集。

頭の体操やIQテストにもってこい！！

シンプルなものから難しいもの、「解けたら天才」な超難問まで。

さっそくチャレンジしてみましょう！

なお、すべての問題は「幼女の論理クイズ」から引用しています。

不思議な消しゴム

ボールペンと消しゴムの値段は合わせて110円。

ボールペンは消しゴムより100円高い。

では、消しゴムの値段は？

今あなたがパッと思い浮かべた答えは

おそらくまちがっています。

正解：
消しゴムの値段は5円

解説：
論理クイズ「2つの文房具」

井戸からの脱出

幼女は深さ30メートルの井戸に落ちてしまった。

幼女は1時間ごとに3メートル登るが、その直後に2メートルずり落ちてしまう。

幼女が井戸から脱出するには何時間かかる？

反射的に答えようとするとミスします。

段階的に考えていきましょう。

正解：
28時間

解説：
論理クイズ「幼女と井戸からの脱出」

消えた1ドル

幼女3人がホテルに泊まることになった。

宿泊料は1人10ドル。
幼女たちは合計30ドルを受付係にわたした。

その後、キャンペーン中なので宿泊料は3人で25ドルだったことに気づいた受付係は、5ドルを返そうとした。

しかし「5ドルは3人で割り切れない」と考えた受付係は2ドルを自分のポケットにしまい、残りの3ドルだけ幼女たちに返した。

さて、幼女たちは1人9ドルで合計27ドル支払ったことになる。
そこに受付係がくすねた2ドルを足して29ドル。

残りの1ドルはどこに消えた？

不思議な感覚におちいる1問。

何が起こっているのか、正確に見抜いてください。

ちなみにこの問題は、当ブログの「論理クイズ」シリーズでもっとも簡単な部類に入ります。

正解：
1ドルは消えていない
問題文にトリックがある

解説：
幼女と消えた1ドル

大きな駐車場

とても大きな駐車場がある。

この駐車場にある車のうち、2台のみ白ではなく、2台のみ青ではなく、2台のみ赤ではない。

駐車場には何台の車があるだろうか？

※各車はそれぞれ一色で塗られている

何やら難しそうに見えますが、視点を変えると解きやすくなります。

正解：
白・青・赤の3台
もしくは「白・青・赤」以外の2台

解説：
論理クイズ「幼女と大きな駐車場」

少なすぎる発言

冷蔵庫のプリンが誰かに食べられてしまった。

幼女Aは「犯人はBです」と発言した。
幼女B,Cもある発言をした。

その後、
『犯人はABCのうち誰か1人』
『犯人だけが発言で本当のことを言った』
ということが分かった。

犯人は誰？

どう考えても情報不足で解けなさそう……。

なのですが、きちんと解けます。

正解：
犯人はC

解説：
論理クイズ「幼女と1人だけの証言」

湖のスイレン

湖にスイレンの花が落ちた。
スイレンは1分経つと2倍に増える。
湖がスイレンでいっぱいになるのに48分かかる。
では、スイレンが湖のちょうど半分になるのに何分かかるだろうか？

有名なクイズ。

「反射的に答えると間違ってしまう」タイプのアレです。

正解：
47分

解説：
世界一短いIQテストがおもしろい！制限時間は60秒

3つの電球

部屋Aには３つのスイッチがある。

部屋Aの3つのスイッチは、部屋Bに置かれた３つの電球にそれぞれつながっている。
ただし、どのスイッチがどの電球に対応しているのかは分からない。

いったん部屋Aから出ると、部屋Bには行けるが部屋Aに戻ることはできない。

あなたは今、部屋Aにいる。

部屋Aの3つのスイッチが部屋Bのどの電球につながっているのかを知りたい。

あなたはどのような行動を取ればいいだろうか？

「頭の体操」的な要素がある論理クイズ。

発想力で解いてください。

正解：
最初に「1つめのスイッチ」だけONにする。
数分経過したのち「1つめのスイッチ」を切り、「2つめのスイッチ」を入れる。

解説：
論理クイズ「幼女と3つの電球」

2頭の馬レース

幼女2人がそれぞれ自分の馬に乗っている。

そこを通りかかった王様がこう言った。

「2人で馬に乗ってレースをしなさい。勝った馬の主の方に宝を与える。ただし、後でゴールした方を勝ちとする」

2人の幼女は相手より先にゴールしないよう、のろのろとレースをしていた。
このままでは、いつまでも勝負がつかない。

だが、たまたま通りかかった賢者の一言を聞いた瞬間、2人はものすごい速度でゴールへ向かっていった。

いったい、賢者は何と言ったのだろうか？

柔軟な発想力がカギになります。

アタマをやわらかくして考えましょう。

正解：
「互いの馬を入れ替えてみて」

解説：
論理クイズ「幼女と2頭の馬レース」

200本の空きカン

ジュースの空きカン5本を集めると、新品のジュース1本と交換してもらえる。

いま、あなたは新品のジュースを200本もっている。

さて、あなたは何本ジュースを飲めるだろうか？

誤答率がかなり高い問題。

ただ、落ち着いて考えれば小学生でも解けます。

正解：
249本

解説：
論理クイズ「幼女と200本の空きカン」

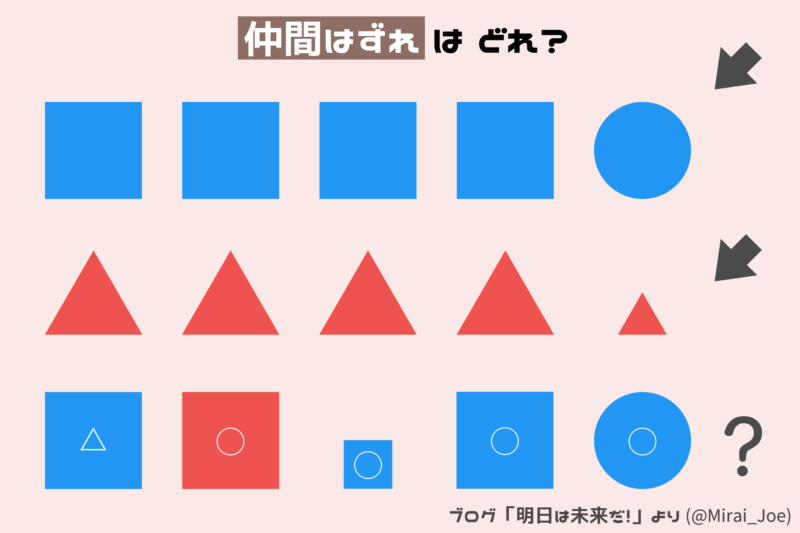
仲間はずれの図形

一番下の列における「仲間はずれの図形」を探してください。

その「理由」も一緒に考えてください。

ちょっとひねった問題です。

正解：
右から2番目の図形

解説：
論理クイズ「仲間はずれの図形」

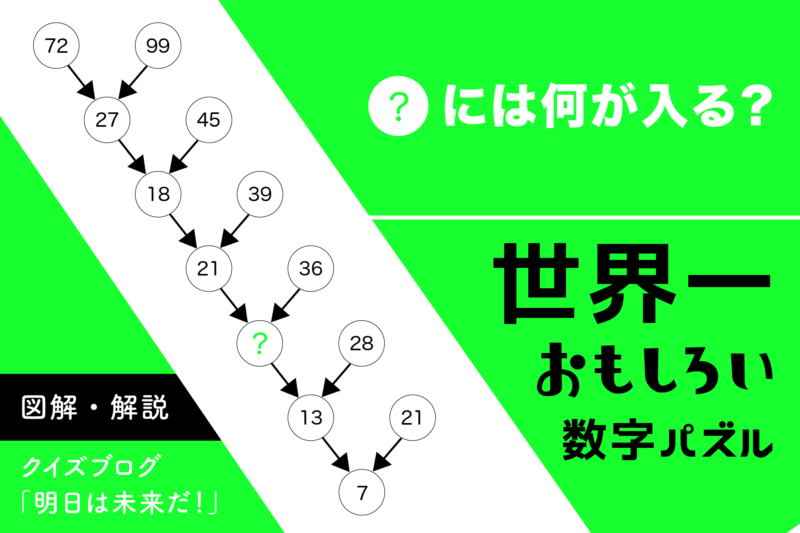
世界一おもしろい数字パズル

ラクに解けそうですか？

最後までよく見てください。

何か、おかしなことが起こっていませんか？

答えは15ではありません。

正解：
12

解説：
世界一おもしろい数字パズルの答えは何でしょう？

3枚のトースト

2枚の食パンを並べて焼けるフライパンがある。

このフライパンを使って、3枚の食パンを両面ともに焼いていく。

食パンの片面を焼くのに30秒かかる。

「1枚目と2枚目を同時に焼く→3枚目を片面ずつ焼く」
という手順だと、3枚全てを焼き終わるのに合計120秒かかる。

もっと短時間で終わらせることはできないだろうか？

ちょっとの工夫で大きな節約。

時短テクは日々の生活に重要です。

正解：
3枚のパンをABCとする
1. AとBの片面を焼く
2. フライパンからBを出してCを入れ、Aの裏側とCの片面を焼く
3. フライパンからAを出してBを戻し、BとCの裏側を焼く
これなら90秒で3枚の両面を焼ける

解説：
論理クイズ「幼女と3枚のトースト」

10回のじゃんけん

幼女A,Bがじゃんけんで10回勝負をした。

Aは、グーを3回、チョキを6回、パーを1回出した。
Bは、グーを2回、チョキを4回、パーを4回出した。
あいこには一度もならなかった。
2人が何の手をどの順番で出したかは分からない。

さて、勝ったのはどちらの幼女だろうか？

ちょっと難しそうですが……。

しっかり考えれば必ず解けます。

正解：
幼女A

解説：
論理クイズ「幼女と10回のじゃんけん」は子供でも楽しめる

手強い10人

10人の幼女がいる。

1人は「正直者」で、それ以外の9人は「気まぐれ」。

「正直者」はいつも本当のことを言う。
「気まぐれ」は気まぐれに本当のことを言ったり完全なウソをついたりする。

今からあなたは1回だけ質問ができる。
ただし、質問できる相手は1人のみ。

たった1回の質問で「10人のうち正直者なのは誰か」を特定しなければならない。

どんな質問をすればいい？

なお、幼女たちは互いの正体を知っている

すこしトリッキー。

「すこし」というか、まあ、ええ。だいぶ。

正解：
「正直者は誰？」

解説：
論理クイズ「幼女と手強い10人」

10枚のコイン

テーブルの上にたくさんのコインが置かれている。

コインは10枚だけが表になっており、残りはすべて裏が上を向いた状態である。

今あなたは、目隠しをした状態でコインを2グループに分ける。
ただし、2つのグループは互いに「表になっているコインの枚数」が同じにならなければいけない。

どうすればよいだろうか？

ぱっと見は「実現不可能」な問題。

目隠しをした状態で、どうすれば解決できるでしょうか。

論理的な答えにたどりついてください。

正解：
まず、コイン全体を「10枚のコイン」と「その他のコイン」に分ける。
次に「10枚のコイン」をすべて裏返す。
これで2つのグループのコインは表の枚数が同じになる。

解説：
論理クイズ「10枚のコイン」

白いボールの箱

箱の中に、ボールが1つ入っている。
ボールの色は、黒か白のどちらかである。

この箱の中へ白いボールをひとつ追加して、箱をよく振ってボールを1つ取り出してみたところ、白だった。

さて、箱の中に残ったボールが白である確率は？

「考えるまでもない」

とっても簡単な問題に思えますが…？

正解：
2/3(約66%)

解説：
論理クイズ「幼女と白いボールの箱」をちょっと考えてみよう

宝石の郵送

Aは箱の中に宝石を入れ、遠く離れた外国にいるBに郵送で宝石を届けたい。

Bがいる国は治安が悪く、南京錠をかけた箱でないと郵送の途中に中身・物品が盗まれてしまう。
南京錠をかければ箱ごと盗まれることはなく安全に郵送することができる。

南京錠はどこにでも売っており、箱にいくらでも南京錠をかけることが可能である。

だが、南京錠・カギ・宝石いずれもそのまま郵送しようとするとそれごと盗まれる。

確実に安全な郵送が保証されるのは「南京錠がかかった箱」と「その中身」のみ。
しかし当然ながら「南京錠のかかった箱」と一緒に「カギ」を送れば箱は開けられ中身が盗まれる。

どうすればAは安全に宝石を郵送できるだろうか。

なお、ABたちはお互い同一の南京錠を持っておらず購入もできない。
また、Aがかけた南京錠のカギをBが保有していることもない。

まったく数字が出てこない名作クイズ。

すばらしく面白い解答が存在します。

自力で解けたらかなり気持ちいいです。

正解：

解説：
論理クイズ「宝石の郵送」

2つのカプセル錠

2種類の固形錠剤AとBがある。

あなたはとある病のため、毎日AとBをきっかり1錠ずつ同時に飲まなければいけない。

ある日、あなたはAのボトルからAを1錠、手のひらに取り出した。
つづいてBのボトルからBを1錠取り出そうとしたが、誤ってBを2錠取り出してしまい、Aと混ざってしまった。

いま、あなたの手のひらには3つの錠剤（Aが1錠、Bが2錠）ある。
AとBは大きさ、匂い、形、重さが全く同一であり、見た目で区別がつかない。

錠剤はとても高価なので、1錠もムダにしたくない。

あなたはどうすればここからA1錠、B1錠を取り出して飲むことができるだろうか？

「柔軟な発想」が必要になるクイズ。

論理的に、しかし頭をやわらかくして考える必要があります。

この状況を解決する方法とは？

正解：

解説：
論理クイズ「2つの錠剤」

ハリーポッターと賢者の石

前には危険　後ろは安全
君が見つけさえすれば2つが君を救うだろう
7つのうちの1つだけ　君を前進させるだろう
別の1つで退却の道が開ける　その人に

2つの瓶はイラクサ酒
残る3つは殺人者　列にまぎれて隠れてる
長々居たくないならば　どれかを選んでみるがいい
君が選ぶのに役に立つ　4つのヒントを差し上げよう

まず第1のヒントだが　どんなにずるく隠れても
毒入り瓶のある場所は　いつもイラクサ酒の左
第2のヒントは両端の　2つの瓶は種類が違う
君が前進したいなら　2つのどちらも友ではない

第3のヒントは見たとおり　7つの瓶は大きさが違う
小人も巨人もどちらにも　死の毒薬は入ってない
第4のヒントは双子の薬　ちょっと見た目は違っても
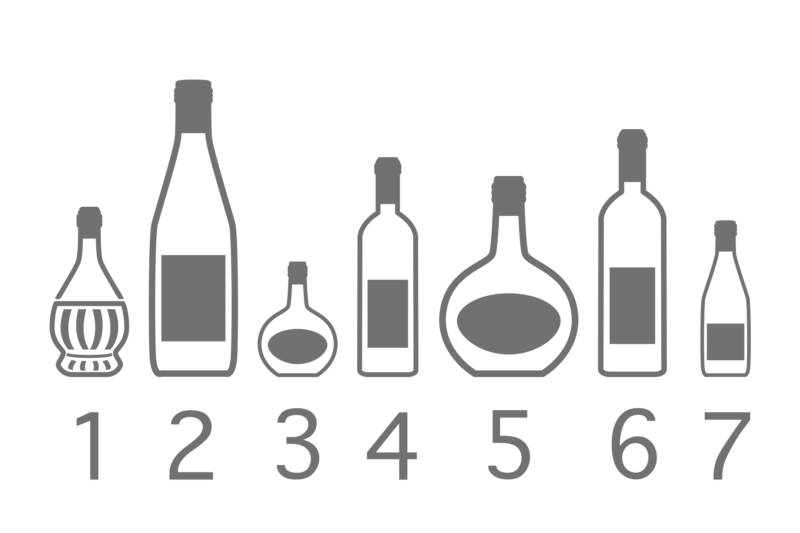
左端から2番目と　右の端から2番目の 瓶の中身は同じ味

7つの瓶にはそれぞれ毒薬・イラクサ酒・前進する薬・退却する薬が入っている。
前進する薬はどれ？

あの有名な『ハリーポッターと賢者の石』の終盤で出題されたクイズです。

原作ではイラストがなかったため解くことができませんでしたが、今回は絵が用意されています。

あなたは解くことができるでしょうか？

正解：
前進する薬は3番

解説：
「ハリーポッターと賢者の石」の論理クイズを解いてみよう

2枚のカード

天使、悪魔、人間の3人がいる。

天使はいつも真実を言う。
悪魔はいつもウソをつく。
人間は真実とウソを交互に言う。どちらを先に言うかは分からない。

幼女は「赤のカード」「青のカード」がたくさん入っている箱を持っている。
幼女は目隠しをしている。

いま、幼女は箱の中からランダムで1枚カードを取り出し、3人に「これは何色？」と聞いた。
A「青」 B「青」 C「赤」

さらに幼女は別のカードを1枚取り出し、同じ質問をした。
A「赤」 B「青」 C「青」

さて、幼女が取り出したカードは何色と何色だろうか？

ただし色の順番まで特定する必要はなく、色の組み合わせだけ特定すればよい。

ABC3人の正体を特定するのではなく、2枚のカードが何だったのかを明らかにする問題。

“色の順番まで指定する必要はない”と書かれているので、「カードの組み合わせ」だけを答えればいいことになります。

すなわち正解は下記のいずれか。

さて。どれでしょう？

正解：
「青」「赤」

解説：
論理クイズ「幼女と2枚のカード」が思ったより手強い

3枚のカード

あなたの目の前に3枚のカードが置かれている。

1枚目のカードは両面が黒、
2枚目のカードは両面が白、
3枚目のカードは片面が黒、もう片面が白で塗られている。

箱の中に3枚のカードを入れてよくかきまぜ、その中の1枚を引き出した。
カードの表面は白だった。

さて、このカードの裏面が白である確率は？

とても有名な問題。

「論理的思考ができるかどうか」をテストする試験でよく使われます。

あなたが出す答えは？

正解：
2/3
(約66.6%)

解説：
論理クイズ「3枚のカード」

4枚のカード

幼女の前に置かれた4枚のカードがある。

「E」「R」「2」「9」

カードにはそれぞれ、片面にはアルファベットが、もう片面には数字が書かれている。

いま、2枚だけカードを裏返して、「母音が書かれたカードの裏には偶数が書かれている」というルールが成立しているかどうか確認したい。

どのカード2枚を裏返せばよいだろうか？

かなり有名な問題。

「見たことがある」という方も多いのでは。

一見すると簡単ですが、よく考えないと正解を逃します。

正解：
「E」と「9」を裏返す

解説：
論理クイズ「4枚のカード」

7つのオーブ

幼女が洞窟に入った。
洞窟は暗いので、ほとんど何も見えない。

この洞窟には、不思議な「7つのオーブ」がある。
オーブにはそれぞれ色がついている。
少なくとも4つ以上のオーブが同じ色である。

同じ色のオーブが触れ合うと、そのオーブはその色に光る。
ちがう色のオーブが触れ合うと、なにも起こらない。

例）
赤のオーブ + 赤のオーブ → 両方とも赤く光る
赤のオーブ + 青のオーブ → なにも起こらない

オーブはとても重い。
そのため、幼女は一度にふたつのオーブしか触れ合わせることができない。

さて、幼女は7つのオーブの中で「もっとも多い色のオーブ」をひとつ持ち帰りたい。

早く洞窟から出たいのでなるべく少ない回数で「もっとも多い色のオーブ」をひとつ特定したいのだが、少なくとも何回オーブを触れ合わせる必要があるだろうか？

洞窟は暗いです。

オーブをくっつけて光らせることでしかオーブの色は分かりません。

「もっとも多い色のオーブ」をひとつ持ち帰るために、何回オーブをくっつければよいでしょうか？

……意外と少ない回数でいけるかもしれません。

正解：
3回

解説：
論理クイズ「幼女と7つのオーブ」

17頭のラクダ

17頭のラクダがいる。

幼女ABCはある人物からこのラクダを受け取ることになった。

ただし条件として、ラクダ全体の頭数のうち
Aは2分の1を
Bは3分の1を
Cは9分の1を
それぞれ受け取らねばならない。

しかし、この条件ではうまく分けることができない。

偶然そこに通りかかった友人は「あること」をしてラクダの分配を条件通りに行った。

さて、友人はいったい何をしたのだろう？

古典的な名問として有名なパズルです。

やや数学的な発想が必要になります。

正解：
友人は、新たにラクダを1頭つれてきてラクダの総数を18にした。
友人は、分割が終わった後に自分のラクダをつれて帰った。

解説：
論理クイズ「幼女と17頭のラクダ」

不思議な昇給

幼女のお給料がアップすることになった。

「プランA」を選ぶと、1年に1回、10万円ずつ昇給していく。
「プランB」を選ぶと、半年に1回、3万円ずつ昇給していく。

「プランA」の給料の支払いは1年に1回、1年分。
「プランB」の給料の支払いは半年に1回、半年分。

さて、幼女はどちらのプランを選ぶべきだろうか？

数学的なセンスを必要とする一問。

ぱっと見は明らかに簡単そうですが……。

正解：
プランB

解説：
論理クイズ「幼女と不思議な給料アップ」

4種類の正直者と嘘つき

ある村には4タイプの幼女がいる。

• 「いつも正直者」の幼女は、いつも真実を語る。
• 「あやしい正直者」の幼女は、いつも真実を語る。ただし例外的に「犯人」の人物を「無実」であると言って嘘をついてしまう。
• 「いつも嘘つき」の幼女は、いつも嘘をつく。
• 「正義の嘘つき」の幼女は、いつも嘘をつく。ただし例外的に「犯人」の人物を「犯人」だと正直に言ってしまう

お気に入りのケーキが幼女A,Bのうちどちらか1人に食べられてしまったので、話を聞いた。

A「私が犯人だよ。Bは正直者だよ」
B「私が犯人だよ。Aが犯人だよ。Aは私と同じタイプだよ」

さて、ケーキを食べたのはどちらの幼女だろうか？

論理クイズの基本とも言える「正直者と嘘つき」パズル。

トリッキーな2タイプが追加されたことで難易度が上がっています。

さて、何から考えればよいのでしょう？

正解：
犯人はB

解説：
難問論理クイズ「幼女と4タイプの正直うそつき村」

パスタのカット

1メートルの長さのパスタがたくさんある。
これから、1本のパスタを切って2つの部分に分けていく。

切る部分が完全にランダムである時、短い方のパスタの長さは平均すると何センチになるだろうか？

むずかしい数学知識は必要ありません。

「何に着目するか」がポイントになります。

正解：
25センチメートル

解説：
論理クイズ「パスタの長さは？」

ミルクとコーヒー

2つのカップA,Bがある。

Aにはミルクが、Bにはコーヒーが入っている。

いま、AのミルクをスプーンですくってBに移す。
Bをよくかきまぜる。
その後、さきほどと同じ量だけBの液体をスプーンですくってAに移す。

このとき、Aの中にあるコーヒーの量は、Bの中にあるミルクの量より多いだろうか？

面白い問題です。

解答を見たらきっと驚きます。

正解：
同じ

解説：
論理クイズ「幼女とミルクとコーヒー」

風の中の飛行機

A,Bという2つの空港がある。

いまから飛行機がAを出発してAB間を往復する。

さて、AB間が「無風」の時にくらべると、「AからBの方向へ常に風が吹いている」時の飛行機の往復時間はどうなるだろうか？

※飛行機のエンジン回転数および風速は常に一定とする

1. 変わらない
2. 無風の時より長くなる
3. 無風の時より短くなる

簡単そうに見えますが、正答率がかなり低い問題です。

「イメージ」と「現実」の乖離を味わえます。

正解：
2. 無風の時より長くなる

解説：
論理クイズ「幼女と逆風の飛行機」

恋人たちの握手

幼女A,Bは恋人同士である。

ABは、4組の恋人たち（合計8人）を招待してパーティーを開いた。

いずれの人間も初対面の人とだけ握手をした。

その後Aは、自分以外のパーティー参加者9人（幼女B+招待客8人）に「何人と握手をしたか」と聞いた。
すると、9人全員が異なる答えを返した。

さて、幼女Bは何人と握手をしたのだろうか？

ウソをついている人はいない。
また、自分自身と握手した人はいない。
さらに、「このパーティーで自分の恋人と初めて会った」という人もいない。

一見すると解答不可能に思える問題。

順を追ってよーーーく考えてみると……。
最初は意味がわからなかった答えにたどりつきます。

正解：
幼女Bは4人と握手した

解説：
論理クイズ「幼女と恋人たちの握手」は小学生向け、だけど難しい

教授のクラス

ある教授が、大学を休むことになった。

しかし自分の代わりに授業をしてくれる人を探していなかったことに気づき、あわてて幼女A,B,Cにメールを送った。

「いきなりだけど私の代わりに誰か1人が授業をやっておいてください！お礼はアップルパイです！」

教授のアップルパイはやたらと美味しいので、幼女ABCは自分が授業をしたいと思っている。

ただし幼女は全員「教授の授業がいつどこのクラスで行われるのか」を知らない。

Aは「クラスの階数」
Bは「授業の時間」
Cは「クラスの学部棟」
のみ知っている。

正解の可能性があるのは、以下のリストの内のいずれか。

• 1階 9時 北館
• 2階 12時 西館
• 1階 3時 西館
• 1階 10時 東館
• 2階 10時 北館
• 1階 10時 南館
• 1階 10時 北館
• 2階 11時 東館
• 3階 12時 西館
• 2階 12時 南館

「授業が行われる場所と時間」をいちばん早く特定した幼女が授業をすることになり、アップルパイを得る。

以下は3人がリストを見た後の会話である。

A「誰か分かった？」
BC（同時に）「Aには分からないよ」
A「あなたたちは分からないの？」
BC（同時に）「分からない」
A「あ、分かった！」

さて、授業はいつどこで行われる？

会話のひとつひとつがヒントになるタイプの論理クイズ。

オーソドックスなものかと思いきや……。

ちょっとまちがえると絶対に解けなくなってしまいます。

正解：
2階 10時 北館

解説：
難問論理クイズ「幼女と教授のクラス」

ダイヤル錠の部屋

3人の幼女が悪魔に閉じ込められた。

悪魔は幼女たちを別々の部屋に入れ、部屋の扉に3桁のダイヤル錠をかけた。

幼女たちは、30分以内にダイヤル錠を解除して部屋から脱出しなければならない。

悪魔は幼女たちに以下のことを告げた。

• すべてのダイヤル錠は、共通の数字で解除できる
• 正解となる数字は「000〜999」のいずれかである
• 3桁の数字を合計すると9になる
• すべての桁の数字が、左の桁の数字以上の数字である
• 一番左の桁を「1桁目」とした時、幼女Aには1桁目を、幼女Bには2桁目を、幼女Cには3桁目を教えた

幼女たちは、いかなるコミュニケーションも取ることもできない。
ただし、「いつ誰がダイヤル錠を解除したか」はリアルタイムで知ることができる。

当初、幼女たちは誰もダイヤル錠を解除できなかった。

ところが、しばらくして誰も解除できなかったのを知った幼女Bは、「正解の数字」が分かりダイヤル錠を解除した。

続いて、それを知った幼女Cがダイヤル錠を解除した。

最後に、2人の様子を知った幼女Aがダイヤル錠を解除した。

いったい、正解の数字は何だったのだろうか？

なお、3人の幼女はいずれも極めて論理的な思考を行うものとする。

劇場版名探偵コナン「ゼロの執行者」の公式ホームページで紹介された有名クイズです。

ポイントとなるのは、登場人物たちの「行動」と「タイミング」。

正解：
(1,1,7)

解説：
論理クイズ「ダイヤル錠の部屋」

関連：
当ブログのクイズが「劇場版名探偵コナン」公式サイトで紹介されました！

隠された得点

3人の幼女が運動会を行う。
参加者は3人のみ。

各競技では1位2位3位にそれぞれ得点が与えられる。
得点は全競技を通して常に一定で、つまり1位は常にX点、2位は常にY点、3位は常にZ点が与えられる。

得点は、X>Y>Z>0を満たす整数である。

いま全競技が終了したところ、

幼女Aは全体で22点
幼女Bは槍投げで1位になり、全体で9点
幼女Cは全体で9点
という結果になった。

さて、100メートル走で2位になったのは誰？

誰もが驚いた問題。

それまで問題文中にまったく現れなかった「100メートル走」の順位について聞かれる難問。

この謎、解けますか？

正解：
100メートル走で2位になったのは、幼女C

解説：
難問論理クイズ「隠された運動会」

シェリルの誕生日

アルバートとバーナードは、シェリルと友達になったばかりです。
シェリルの誕生日を2人は聞きましたが、彼女は10の日にちを候補としてあげました。

5月15日、5月16日、5月19日
6月17日、6月18日
7月14日、7月16日
8月14日、8月15日、8月17日
それから、シェリルは、アルバートに「月」だけを、バーナードに「日付」だけをそれぞれ教えました。

アルバート「僕はシェリルの誕生日を知らないけど、バーナードも知らないよ」

バーナード「僕はシェリルの誕生日を知らなかったけど、今は知っているよ」

アルバート「それなら僕もいつだか知っているよ」

シェリルの誕生日はいつでしょうか？

少し前に話題になった超難問算数クイズ「シェリルの誕生日」を元にした問題。

14〜15歳向けに出題されたこの問題が、「大人でも解けない」と評判になりました。

論理的な答えがきちんと存在します。

ひとつずつ考えていきましょう。

正解：
7月16日

解説：
難問論理クイズ「幼女とシェリルの誕生日」

草原の兵士たち

草原に兵士たちが立っている。
人数は奇数。

兵士間の距離はすべてバラバラである。

兵士たちは、自分から一番近い兵士だけをずっと見ているように言いつけられている。

このとき、誰からも見られていない兵士が必ず1人はいるらしいのだが本当だろうか。

本当でも嘘でも、論理的に証明してほしい。

少し変わった問題です。

いかにも簡単に解けそうに見えますが、意外と手強いことにすぐ気づきます。

あなたの「着眼センス」が問われます。

正解：
本当。
この条件では、誰からも見られていない兵士が必ず1人は存在する。（証明は後述）

解説：
論理クイズ「幼女と草原の風」

【難問】 2か国製の機械

どんな質問に対しても「はい」「いいえ」で正しく答える機械がある。

この機械は緑か赤のライトを点灯させて「はい」「いいえ」を表現する。

一方の色が「はい」、もう一方の色が「いいえ」を表す。

A国とB国がこの機械をつくった。

一方の国でつくられた機械は、緑が「はい」、赤が「いいえ」を表す。
もう一方の国でつくられた機械は、緑が「いいえ」、赤が「はい」を表す。

ただし、緑が「はい」を示す機械がA国製なのかB国製なのかは分かっていない。

いま、幼女の目の前に1台の機械がある。
幼女はそれがABどちらの国でつくられたのかを知りたい。

「はい」「いいえ」で答えられる質問を1回だけ機械にすることができる。

どんな質問をすればいい？

まさに論理クイズ。

「死ぬほど難しい」というわけではないので、ぜひ時間を割いて考えてみてください。

正解：
「A国製の機械は、緑のライトが「はい」を表すか？」

解説：
難問論理クイズ「幼女と2か国の機械」

【難問】 ルーシーの数字

あなたはパーティー会場にいる。
ルーシーと幼女の会話が聞こえてきた。

どうやらルーシーは「1〜100」のうち、いずれかひとつの数字が書かれた紙をもっているようだ。

ルーシーは幼女に言った。

「私に次の4つの質問をしてね。その答えで私の持っている数字が分かるよ」

・その数字は2で割り切れる？
・その数字は3で割り切れる？
・その数字は5で割り切れる？
・その数字は7で割り切れる？

ルーシーは、「私の数字は◯で割り切れるよ」というように4つの質問の答えを幼女にこっそり教えていった。

ゴキゲンなパーティー参加者がうるさいので、残念ながらあなたが聞き取れたのは4つの答えのうち1つだけだった。

しかし、それを聞いて「なるほど。その数字で割り切れるんだな」と分かった瞬間、あなたはルーシーの持っている数字が何なのか分かった。

いったいルーシーの数字は何だろう？

なお、ルーシーはつねに真実を語る。
また、あなたはきわめて論理的な存在である。

少なすぎるヒントに惑わされる一問。
正解の候補となる数字は、ちょっと盲点になりやすい所からしぼりこんでいきましょう。

正解：
70

解説：
難問論理クイズ「幼女とルーシーの数字」のヒントが少なすぎる

【難問】33%の帽子

幼女A,B,Cが帽子をかぶらされ、円形に座っている。

幼女たちはお互いにコミュニケーションがとれない。

帽子の色は「赤」か「青」か「白」。
3人とも赤、3人ともちがう色、というパターンもありえる。
自分の帽子の色は見えないが、自分以外の2人の帽子の色は見える。

いま、3人の幼女は同時に「自分の帽子の色」を宣言する。
このとき、3人のうち少なくとも1人が正解しなければならない。

幼女たちは帽子をかぶらされる前に相談ができる。
どのような戦略をとればいいだろうか？

状況はわりとシンプル。

ですが、しっかり解こうとするとかなり難解です。

「なぜそれで正解になるのか」まで答えられたら、相当高度な論理力をお持ちです。

正解：
帽子の色を
赤 = 0
青 = 1
白 = 2
と数字に置きかえる。
それぞれの幼女は、3人の合計が（0,3,6）もしくは（1,4）もしくは（2,5）になるように自分の色を宣言する

解説：
難問論理クイズ「幼女と33%の帽子」でさらに正解を探せ

【難問】 不可能な数字当て

AとBがゲームを行う。

AもBもそれぞれ、「連続する2つの数字（正の整数）のうちどちらか」を与えられる。

ただし、相手の数字は分からない。

たとえばAが20、Bが21を得たとする。
Aは「Bの数字は19か21」ということしか分からない。
Bも「Aの数字は20か22」ということしか分からない。

AとBは互いにコミュニケーションを取れない。

また、ゲームが始まる前に戦略を練ることもできない。

ゲーム開始から1分経過するごとに（毎分）鐘が鳴る。

鐘が鳴ったら、ABは「相手の数字を推測して答える」「沈黙したまま待機する」のどちらかの行動を取れる。

ゲームは、どちらかの人物が1回でも「相手の数字を推測して答える」行為を行った時点で終了する。

相手の数字を正確に当てることができた人物がゲームの勝者となるが、間違えれば敗者となる。

さて、A（もしくはB）がこのゲームに勝つために行う最適行動とは？

ただし、2人ともパーフェクトに論理的な思考をする。

意表を突く問題。

「論理も何もない」
「ただの運ゲーだ」
と思ってしまう気持ちを抑えて、よく考えてみてください。

ゲームに勝つための最適行動が、実は存在します。

正解：
小さい方の数字を与えられた人物が、「自分の数字の回数」分の鐘が鳴った瞬間に相手の数字を言い当てる

解説：
難問論理クイズ「幼女と不可能な数字当て」

【難問】 色の見えない帽子

箱の中に、赤い帽子が2つ、緑の帽子が3つある。

ABCの3人は、目をつぶって箱の中から帽子を取り出してかぶっていく。

お互いの帽子を見ることはできるが、自分の帽子を見ることはできない。
箱の中にあった帽子の内訳は全員が知っている。

ABCに対し「自分の帽子の色が分かるかどうか」を順に質問したところ、以下のような回答を得た。

A「わからない」
B「わからない」
C「わからない」
A「わからない」

ABCはいずれも論理的である。

ただし、ある人物1人だけが赤と緑の区別がつかない（赤と緑の帽子が同じ色の帽子に見える）

「赤と緑の区別がつかない幼女が誰なのか」は全員が知っている。

さて、「赤と緑の区別がつかない」のは誰だろうか？

そして、その人物の帽子の色は？

論理クイズとしてはメジャーな「帽子問題」です。

しかし、「色がわからない人がいる」という一点がとても特徴的で斬新。

あらゆる仮定を駆使して答えに迫ってください。

正解：
「赤と緑の区別がつかない人物」はBで、Bの帽子の色は緑色

解説：
論理クイズ「幼女と色の見えない帽子」

【難問】 過半数の名は

ある投票が行われた。

投票された幼女の名前が1票ずつ読まれていく。

いま、投票数の過半数（全体の半分より多い数）を得た幼女がいるならば、その名前を特定したい。

しかしあなたが持っているのは1ずつ数字を増減できるカウンターのみ。
さらに、あなたは同時に1つの名前しか覚えられない。

どうすればよいか？

いかにも簡単そうに見える一問。

ですが、考えてみると予想以上に難しいことに気づきます。

この制限された状況で可能なこととは？

正解：
・開始時にカウンターを0にセット
・カウンターが0の時、「聞いた名前」を記憶してカウンターを+1
・カウンターが1以上の時、「聞いた名前」が『記憶している名前』と同じだったらカウンターを+1する
・カウンターが1以上の時、「聞いた名前」が『記憶している名前』とちがったらカウンターを-1する ※ただし『記憶している名前』はそのまま

解説：
論理クイズ「幼女と過半数のカウント」

【難問】 失われた搭乗券

100人乗りの飛行機がある。

100人の乗客たちは自分の座席番号が書かれたチケットを持っている。

だが、搭乗1人目の乗客はチケットを紛失したので、ランダムで選んだ席に勝手に座ってしまった。

2人目以降の乗客は、自分の席が空いているならそこに座り、空いていない場合には空席をランダムに選んで勝手に座る。

いま、最後の乗客（100人目）が飛行機に乗り込んだ。
この人物が自分のチケットの席に座れる確率は？

わりと難問。

普遍的な視点が必要になります。

問題をシンプルにする方法はないでしょうか？

正解：
50%

解説：
難問論理クイズ「幼女と失われた搭乗券」

【難問】 クラリスの誕生日

A、B、クラリスの3人は友人である。
全員とても論理的で、つねに真実を話す。

AとBは、クラリスの誕生日の『月』も『日』も知らない。
そこでクラリスは次の方法で教えることにした。

まずクラリスが、AとBに聞こえるように叫ぶ。
「私の誕生日の『日』の数字は、私の誕生日の『月』の数字以下だよ」

それからクラリスはAに『日』を、Bに『月』を教えた。

A「Bはクラリスの誕生日が分からないよ」
B「Aもクラリスの誕生日が分からないよ」

2人はまったく同じ会話を何回も繰り返したが、最後に

A「Bはクラリスの誕生日が分からないよ」
B「いま、私たちはクラリスの誕生日が分かっている」

と発言して終わった。

結論から言うと、2人の「まったく同じ会話」は考えうる限りもっとも多く繰り返された。

クラリスの誕生日はいつだろうか？

「シェリルの誕生日」
「チャーリーの誕生日」
と同系統の問題……。

かと思いきや、使われているロジックはかなり異なります。

解けたら友人に自慢できるレベル。

正解：
7月7日

解説：
難問論理クイズ「幼女とクラリスの誕生日」

【難問】 シュレディンガーの猫

1〜5の番号が書かれた5つの箱がある。
箱は1,2,3,4,5の順で一列に並んでいる。

ネコはこの箱のどれか1つに隠れており、夜になると必ずひとつだけ隣の箱に移動する。

朝になった時、幼女は1つだけ箱を調べて、そこにネコがいるかどうか確認できる。

さて、いつか幼女はネコを見つけられるだろうか？

不可能に思える難問。

グーグルやマイクロソフトなどの世界的大企業の入社試験に出題されたこともあります。

論理的思考で収束させてください。

正解：
できる。
最適な行動を行えば、遅くとも6日目にはネコを発見できる。

解説：
難問論理クイズ「幼女とシュレディンガーの猫」

【難問】 イースターエッグの箱

以下のように3×4の箱が並んでいる。

この12の箱のうち、ランダムに選ばれたどれか2つの箱にイースターエッグが1つずつ入っている。
残り10の箱は空である。

箱にはそれぞれA〜Lのラベルが貼られている。

A	B	C	D
E	F	G	H
I	J	K	L

いま、2人の幼女が同時に1つずつ箱の中身を確認していく。

幼女アリスは、A, B, C, D, E, F, G, H, I, J, K, L,の順で。
幼女イヴは、A, E, I, B, F, J, C, G, K, D, H, L,の順で。

イースターエッグを1つでも先に見つけた方が勝者となる。

たとえばイースターエッグがB,Cに入っていた場合、2番目の箱でそれを発見できるアリスが勝者となる。

さて、このゲームで有利なのはどちらの幼女だろうか？

なお、同時に見つけた場合は引き分けとなる。

一見してもちょっと意味が分かりません。

有利もなにも、勝率は五分五分なのでは？

発想力と分析力がためされる問題です。

正解：
アリスの方が有利

解説：
難問論理クイズ「幼女とイースターエッグの箱」でナゾを解く

【難問】 キャリバンの遺言状

キャリバンの遺言状にはこう書かれている。

「私が持っている10冊の本を、幼女A,B,Cにあげます」
「ただし次の順番で幼女を選んでわたしてください」

1. 私と会ったときに白い帽子をかぶっていた幼女を、Aより先に選んではいけません
2. 幼女Bが1920年にオックスフォード（※英国の街）を旅行しなかったのであれば、「1番目に選ぶべき幼女」は私に傘をかさなかった幼女です
3. 幼女BまたはCが「2番目」に選ばれるとしたら、Cは”3人の中でもっとも早く初恋を経験した人”よりも先に選ばれなければいけません

残念ながら幼女ABCは、遺言状に書かれていることをまったく覚えていなかった。

キャリバンの関係者はこう言った。
「”この遺言状には不必要な文章がひとつもない”と仮定すれば、本を渡す順番は必ず分かる」

さて、ABCが本を受けとる順番は？

ヒントっぽいけどヒントじゃない。

何を手がかりにして考えればいいのか全く分からない難問です。

答えは出ます。
かなり論理的に解かないとむずかしいですが。

正解：
本がわたされる順番は「A,C,B」

解説：
難問論理クイズ「幼女とキャリバンの遺言状」は意味不明に思えるけれど

【難問】 3色のカメレオン

3色のカメレオンがいる。

青のカメレオンは13匹。
赤のカメレオンは15匹。
緑のカメレオンは17匹。

色が異なるカメレオン2匹が触れ合うと、どちらも第3の色に変化する。
例：青のカメレオンと赤のカメレオンが触れ合う→両者とも緑のカメレオンに変化する

さて、このカメレオンたちを1箇所に閉じ込めたとき、すべてのカメレオンの色が同じになることはありえるだろうか？

難問。

数学の知識は必要ありませんが、数学的センスが要求されます。

いかにも簡単そうに見えるクイズの本質はどこにあるのか？

正解：
すべてのカメレオンが同じ色になることは、ありえない

解説：
難問論理クイズ「幼女と3色のカメレオン」

【難問】 4タイプの正直者とウソつきの島

ある島には4タイプの幼女がいる。

• 「いつも正直者」の幼女は、いつも真実を語る。
• 「ごまかす正直者」の幼女は、いつも真実を語る。ただし例外的に、自分が「犯人」の場合は「自分は無実だ」という嘘をついてしまう。
• 「いつも嘘つき」の幼女は、いつも嘘をつく。
• 「正義の嘘つき」の幼女は、いつも嘘をつく。ただし例外的に、自分が「犯人」の場合は「自分は犯人だ」と正直に言ってしまう。

この島で「冷蔵庫のプリンが勝手に食べられる事件」が起きた。
目撃者によると犯人は1人。
その時間に犯行が可能だったのは、幼女A,B,Cの3人のみ。

A「私は無実だよ。Bが犯人だよ。Bは正直者だよ」
B「私は無実だよ。Aが犯人だよ。Cは私とはちがうタイプだよ」
C「私は無実です。Aが犯人です」

さて、プリンを食べた幼女は誰だろうか？

先に出てきた「4種類の正直者と嘘つき」のクイズに似ていますが、こちらが本番。

論理力のみならず、思考力のすべてを使わねば解けない問題。

解けたらかなりの頭脳の持ち主です。

悩んで悩んで、どれだけ考えても解けなくて、それでも正解にたどりついた時の爽快感は随一。

個人的にはもっとも面白い論理クイズだと思っています。

超おすすめです。

ぜひノーヒントで挑戦してください。

正解：
長くなるので省略。
解説記事を見てください。

解説：
難問論理クイズ「幼女と4タイプの正直うそつき島」

【難問】 謎のパーティー

あるパーティーに3人の幼女A,B,Cが招待された。

以下は、幼女たちの発言である。

パーティー2日前：
幼女A「Bはパーティーに行くよ」
幼女B「Cはパーティーに行かないよ」
幼女C「私が出席する場合だけAもパーティーに行くよ」

パーティー1日前：
幼女A「私が欠席するならCは出席するよ」
幼女B「私たち3人の中でパーティーに行くのは偶数人数だよ」
幼女C「Aはパーティーに行くよ」

パーティー当日：
幼女A「まだ2018年にはなってないよ」
幼女B「私が行くときだけAも行くよ」
幼女C「3人のうち少なくとも1人はパーティーに行かないよ」

この3人の幼女については以下の事実が判明している。

1人だけ絶対に嘘をつかない幼女がいる。

別の1人は、今日が2で割り切れる日なら嘘をつく。それ以外の日なら真実を言う。

残る1人は、今日が3で割り切れる日なら嘘をつく。それ以外の日なら真実を言う。

問題
(1) パーティーに出席する幼女は誰？
(2) パーティーの日程が将来だとすると、開催は西暦何年の何月何日だろうか？

※問題文が発表されたのは2015年8月18日である

きわめて面白い難問。

問題文は長いですが、ぜひチャレンジしてください。

ビックリするような正解が隠れています。

正解：
長くなるので省略。
解説記事を見てください。

解説：
難問論理クイズ「幼女と3人のパーティー」

【難問】 石像の部屋

23人の幼女が、ある館に閉じ込められた。

この館には「石像の部屋」がある。
「石像の部屋」には石像が置いてあり、東西南北のいずれかを向いている。

幼女たちはそれぞれ個室に閉じ込められており、互いに連絡を取り合うことはできない。

悪魔は幼女を1人ランダムに選んで、石像の部屋につれてくる。
誰がいつ選ばれたかを他の幼女は知ることができない。

石像の部屋につれてこられた幼女は、以下の行動をどれかを必ず実行しなければならない。

• 石像を左に90度回転させる
• 石像を右に90度回転させる
• 石像を壊す

幼女が石像を回転させた場合､その幼女は個室に戻され、次にランダムに選ばれた幼女が石像の部屋につれてこられ、同様の操作をする(以下繰り返し)。

幼女が石像を壊した場合、石像の部屋に一度でも入ったことのある幼女全員が解放される。

23人全員の幼女が確実に解放されるには、どのような戦略を取ればよいか？

幼女たちは、ルールを知った上で開始前に戦略を練ることができる。

幼女が石像の部屋に呼び出されるタイミングだが、同じ幼女が連続して呼び出されることもある。
ただし、どの幼女も充分な時間を待てば必ず何度でも呼び出されるものとする。
しかし、「充分な時間」がどれほどの時間なのかは分からない。

また、幼女たちは石像の最初の向きを知らない。

かなりの難問。

きわめて高度な論理力が必要になります。

解ける人はめっちゃ頭いいです。

ちなみに、解法がとても面白い一問です。

正解：
長くなるので省略。
解説記事を見てください。

解説：
難問論理クイズ「23人の幼女と石像の部屋」

【超難問】 3人の神

真神、偽神、乱神という3人の神がいる。

真神は常に真実を語る。
偽神は常に嘘をつく。
乱神はランダムで真実を言ったり嘘をついたりする。

3人の神は、外見では見分けがつかない。

あなたはこれから、「はい」か「いいえ」で答えられる質問を3回だけ行って、3人の神の正体を完全に特定したい。

各質問はそれぞれ1人の神に対して行う。
質問ごとに相手を変えてもよい。

質問に対して3人の神は「ダー」「ヤー」という返答をする。

「ダー」「ヤー」は「はい」「いいえ」を意味する言葉だが、「ダー」「ヤー」のどちらが「はい」「いいえ」なのかは分からない。

あなたはどのように質問すればよいだろうか？

ただし、神は互いの正体を知っている。

超難問。

どう考えても不可能に思えます。

発表当時、世界中のクイズ愛好家・数学者が「どう考えてもムリ」と頭を抱えた伝説の難問。

あなたは歴史に打ち勝てるか。

正解：
長くなるので省略。
解説記事を見てください。

解説：
超難問論理クイズ「幼女と3人の神」

【超難問】 7枚のカード

1〜7の数字が書かれた7枚のカードがある。
これをよくシャッフルして幼女ABCの3人に以下のように配る。

幼女Aにはカード3枚
幼女Bにはカード3枚
幼女Cにはカード1枚

まず、幼女Aは自身のカードを見て、何らかの「真実（であると認識していること）」を宣言する。

続いて、幼女Bも自身のカードを見て、何らかの「真実（であると認識していること）」を宣言する。

これらの宣言は全幼女に聞こえる。

いま、これらの行動が行われたところ、幼女Aは幼女Bのカードが何なのかを完全に把握した（すなわち「Cのカードが何なのか」も分かった）。
同様に、幼女Bも幼女Aのカードが何なのかを完全に把握した（すなわち「Cのカードが何なのか」も分かった）。

だが、全く同じ情報を聞いていたはずの幼女Cは誰が何のカードを持っているのかが分からないままだった。

いったい、AとBはどのようなことを言ったのだろうか？

なお、「AとBが事前に打ち合わせること」「AとBの間でのみ通じる暗号を使う」「Cにバレないように上記以外の何らかのコミュニケーションを取ること」は禁じられている。

最後に、すべての幼女はきわめて論理的である。

当ブログの「論理クイズ」シリーズにおいて、最難関レベルにある一問。

かなり頭が良い人でも、解決の糸口すらつかめない。かもしれません。

驚くような解決法とは？

正解：
長くなるので省略。
解説記事を見てください。

解説：
超難問論理クイズ「幼女と7枚のカード」

【超難問】 チェス盤の部屋

チェス盤が置いてある部屋があります。

悪魔はこのチェス盤の8×8のマスに無数のポーンをランダムに置いていきます。
悪魔は完全に気まぐれにポーンを置くため、64マス全てにポーンを置いたり、逆に1つもポーンを置かなかったりするかもしれません。
なお、各マスに置けるポーンの数は1つです。

この部屋の外に幼女Aと幼女Bを待機させています。
悪魔は幼女Aだけをチェス盤の部屋に入れて、1以上64以下の整数のどれかひとつを告げます。

幼女Aはチェス盤の上に
1. ポーンが置いていないマスに1つだけポーンを置く
2. ポーンが置いてあるマスから1つだけポーンを取り除く
のいずれかの操作を1回だけ行います。
何もしないということは許されません。

その後、悪魔は幼女Bをチェス盤の部屋に入れます。
幼女Bはチェス盤の様子を見て幼女Aに告げられた整数を当てなければなりません。
回答のチャンスは1回のみ。

幼女たちはどのような戦略を取ればよいでしょう。
なお、幼女たちは初めのチェス盤の様子を知りません。

ただし、幼女たちはルールを知った上で開始前に戦略を打ち合わせることができます。

史上最強の超難問。

あらゆる論理クイズの頂点に位置する問題。

「高度な専門知識を用いずに解ける問題」としては、確実に歴代一位の難易度です。

解けたら間違いなく天才。

全力で挑戦してみましょう。

正解：
長くなるので省略。
解説記事を見てください。

解説：
超難問論理クイズ「2人の幼女とチェス盤の部屋」

まとめ

いかがでしたか？

普通のクイズとは違って、「ひっかけ」「言葉遊び」「知識勝負」といった要素がない、きわめて論理的なクイズ。

この他にもいろいろ面白いクイズがあるので、ぜひ「幼女の論理クイズ」シリーズをチェックしてください！