たぶんこれが世界一難しい論理クイズです。
ぼくは論理パズルや論理クイズが好きでよく探しているのですが、今回見つけたこの問題の難易度は過去最高級でした。
ぱっと見は簡単なのに、少し考えてみると異様に難しくて突破口すら見えない。
そんな悪夢のようなクイズをお楽しみください。
問題
チェス盤が置いてある部屋があります。
悪魔はこのチェス盤の8×8のマスに無数のポーンをランダムに置いていきます。
悪魔は完全に気まぐれにポーンを置くため、64マス全てにポーンを置いたり、逆に1つもポーンを置かなかったりするかもしれません。
なお、各マスに置けるポーンの数は1つです。
この部屋の外に幼女Aと幼女Bを待機させています。
悪魔は幼女Aだけをチェス盤の部屋に入れて、1以上64以下の整数のどれかひとつを告げます。
幼女Aはチェス盤の上に
1. ポーンが置いていないマスに1つだけポーンを置く
2. ポーンが置いてあるマスから1つだけポーンを取り除く
のいずれかの操作を1回だけ行います。
何もしないということは許されません。
その後、悪魔は幼女Bをチェス盤の部屋に入れます。
幼女Bはチェス盤の様子を見て幼女Aに告げられた整数を当てなければなりません。
回答のチャンスは1回のみ。
幼女たちはどのような戦略を取ればよいでしょう。
なお、幼女たちは初めのチェス盤の様子を知りません。
ただし、幼女たちはルールを知った上で開始前に戦略を打ち合わせることができます。
さあ、解いてみよう!
問題文は以上です。
がんばってください。
文章自体はとてもシンプルです。
一見すると「どう考えても解答不可能」な問題ですが、ちょっと考えてみればやっぱり無理っぽくて、よくよく考えてみても確実に不可能のように思えます。
以下の章は「重要なポイント」「ヒント編」「解答編」という構成になっています。
ノーヒントで解きたい方は「重要なポイント」を読むだけにしましょう。
どうしても分からない方は「ヒント編」以後を少しずつ読み進めていってください。
正直なところこの問題は本当に難しく、これをノーヒントかつ短時間で完全に解ける方は……1万人に1人くらい……なのではとすら思ってしまいます。
10分であきらめるのも手です。
ちなみにぼくは5分で降参しました。
それでは問題のポイントを見ていきましょう!
重要なポイント
チェス盤の初期状態
悪魔はこのチェス盤の8×8のマスにポーンをランダムに置いていきます。
なお、幼女たちは初めのチェス盤の様子を知りません。
悪魔は気まぐれに64マスにポーンを置いていきます。
あるマスに置いて、あるマスには置かなかったり。
全部のマスに置いたり、1つも置かなかったり。
これは完全にランダムなので、あらゆる可能性が考えられます。
そして幼女たちは事前にその配置を知ることができません。
ポーンの配置方法は264通り、すなわち1844京6744兆737億955万1616通りです。
1秒に1通りの配置を覚えたとしても、すべて覚えるには約5850億年かかります。
つまりゲーム開始前に、チェス盤のあらゆる初期状態に対応できる何らかの戦略が必要不可欠になるのです。
告げられる整数
悪魔は幼女Aだけをチェス盤の部屋に入れて、1以上64以下の整数のどれかひとつを告げます。
幼女Bはチェス盤の様子を見て幼女Aに告げられた整数を当てなければなりません。
悪魔が指定する整数は1~64のどれかですが、どれになるのかは完全にランダムなため事前に予測することは不可能です。
この論理クイズは、幼女Bが悪魔の指定した整数を当てれば解決します。
しかし、正解となるその整数は幼女Aにしか告げられません。
幼女Aは指定された整数を幼女Bに伝えるためランダムなチェス盤に1回だけ操作を加え、幼女Bはそのチェス盤の状況を見て正解となる整数を当てるしかないのです。
幼女Aの操作
幼女Aはチェス盤の上に
1. ポーンが置いていないマスに1つだけポーンを置く
2. ポーンが置いてあるマスから1つだけポーンを取り除く
のいずれかの操作を1回だけ行います。何もしないということは許されません。
この論理クイズにおいて、幼女側が状況を変えられる唯一の選択肢。
それが、チェス盤のマスにポーンを置く、あるいは取り除くという幼女Aの操作です。
ただし、操作できるのは1回だけ。
1つのポーンのみ。
64マスのどれか1マスにたったひとつのポーンを加え(あるいは減らす)ことしか許されません。
そのあまりに少ない操作で、何とか情報を伝えなければならないのです。
繰り返しになりますが、チェス盤のポーンの配置は完全にランダムです。
さらに厄介なことに、幼女Aには「何もしない」という選択肢が許されていません。
仮に幼女たちが「この配置だったら53ということにしよう!」と打ち合わせ、幼女Aが部屋に入ってチェス盤の配置が打ち合わせどおりの53の配置だと気づき、かつ悪魔が正解の数字に53を指定したとしても、幼女Aは必ずどこかのマスにポーンを置いたり取り除いたりしなければならないため、打ち合わせていた53の配置が崩れてしまいます。
幼女たちが行える唯一の操作は、大変トリッキーな性質を有しているのです。
情報量の少なさ
幼女Bはチェス盤の様子を見て幼女Aに告げられた整数を当てなければなりません。
最大のポイントとなるのが、幼女たちが得られる情報の少なさ。
幼女Bがチェス盤に置かれたポーンの初期状態を知ることは原理的に不可能です。
なぜなら、幼女Bが得られる情報はチェス盤の様子のみですが、その時のチェス盤の状況は必ず幼女Aによる変更が加えられた後のものだからです。
幼女Aがチェス盤に置かれたポーンの初期状態を幼女Bに伝えることも原理的に不可能です。
なぜなら、幼女Aはどこか1マスのポーンを動かすことしかできず、「どのポーンを動かしたのか」までは伝えようがないからです。
幼女Bが「2つのポーンが置かれているチェス盤」を見たとき、彼女はそれが「元々ポーンは3つだったのか」「元々ポーンは1つだったのか」を判別できません。
幼女たちが得られる情報はきわめて限定されています。
のみならず、幼女Aと幼女Bの間ですら決して伝えられない情報が存在するのです。
ヒントの前に
以上が問題のポイントとなる箇所です。
当然ですが、ここに述べられなかった重要な点があるかもしれませんし、列挙したものすべてが直接解答に役立つとも限りません。
あまり書いてしまうとヒントになってしまいますので。
この次の項から「ヒント編」が始まります。
最初は漠然としたヒントですが、次第に核心に迫るものに変わっていきます。
では、どうぞ。
ヒント編
第1のヒント
この問題には、正解が存在する
最初に申し上げますが、この問題にはきちんと解答が存在します。
それは言葉遊びや理不尽な答えではなく、極めて論理的に100%正解になる解答です。
ある意味これ自体が大きなヒントになります。
「きちんと解ける問題だとしたら、どの時点でどういう状況になっていなければいけないか?」を逆算して考えていくのがポイントです。
第2のヒント
正解は極めて難解かつ複雑なものである
ヒント編になったので早々にぶっちゃけますが、「解答準備編」「解説編」「正解編」の文字数だけで10000文字を超えます。
それだけの文章を書かねばならない解答、というわけです。
どれくらい難解かつ複雑なのかと言うと、解答を見ても「何言ってるか全然わからない」と思う人が出てきてもおかしくないレベルです。
ただし、いろいろと極限まで頑張れば、「正解文」自体は3行以内に収まります。それが理解可能かは別として。
第3のヒント
解答するには、ほぼ専門的な3つの知識が必要になる
本問は、論理クイズにありがちな「ちょっと頭をひねれば誰にでも解ける」ようなものではありません。
解答に際しポイントとなる知識は3つありますが、そのいずれも「知っていなければ分からない」と言っていいレベルのものです。
全く知らない方がゼロから思いつくのは……理論的には不可能ではないかもしれませんが……ほぼ不可能です。
さらに言うと、その3つの知識をこの問題に応用する飛びぬけた発想力も必要になってきます。
ちなみに「ほぼ専門的な3つの知識」ですが、ある職業の方々なら基本的な知識としてご存知のはずです。
なお、3つの知識のうち2つは重複するところが多いので、2つの知識で解けると言っても一応は過言ではありません。
第4のヒント
64マスでさえあれば、チェス盤である必要はない
シンプルな問題文とエレガントな解答を持つ本論理クイズですが、たったひとつだけ落とし穴があるとするなら、タイトルにも登場しいかにも象徴的な意味を持っていそうな「チェス盤」にあまり意味がないこと。
さらに言えば、置かれているコマもポーンである必要もありません。
将棋の駒でも、なんならコインでも本問は成立します。
重要なのは、64マス状の盤であること。
第5のヒント
幼女Aと幼女Bはチェス盤の状況を活用する
重要なヒントです。
幼女たちが行える行動・および得られる情報はかなり限定されています。
幼女Aが幼女Bに情報を伝えるためにできることは?
鍵となるのはチェス盤のポーンの状況です。
第6のヒント
幼女Aの操作のポイントは、任意の1マスのポーンの「有」「無」状態を切り替えられること
最初に多くの方が考える「幼女Aの操作の意味」。
マスにはポーンが「有る」状態と「無い」状態しかありえません。
幼女Aは、1回だけ必ずどこかのマスの状態を逆側に切り替えられます。
それだけの操作でこの問題が解けるとしたら、操作の他にやるべきこととは……?
第7のヒント
幼女たちは、計算を行う
どう考えても不可能に思えるこの問題を解決するのは、これが論理クイズであるという大前提。
論理クイズである以上100%正解になる解答が存在し、そして「どのマスのポーンをどのように操作するか」という選択肢が与えられている以上、「幼女Aの操作」に確実な意味を持たせる何らかの方法が存在するはずです。
それが計算です。
幼女たちの解答のプロセスは、その多くが計算によって占められます。
第8のヒント
幼女たちは、チェス盤のマスに0~63の整数を割り振る
非常に大きなヒントです。
大部分の方がまず「チェス盤のマスに1〜64の数字を割り振る」というアイデアを思いついたことでしょう。
しかし、実際に割り振るべきなのは0〜63の数字です。
なぜなのかは解答の早い段階で分かります。
どちらも64個なので個数としては変わりませんが、ここに至れるかどうかが最初の難関です。
第9のヒント
幼女Aと幼女Bは、計算を行い、チェス盤の状況を数値化する
きわめて重大なヒントです。
というか「これがすべて」と言っても構いません。
この論理クイズは、幼女たちがチェス盤の状況を数値化するその方法が何なのかという疑問にすべての要素が集約しています。
今一度だけ考えてみてください。
幼女Aはチェス盤の数値化とポーンの操作を行います。
幼女Bもチェス盤の数値化を行います。
……ならば、チェス盤の数値化とはどのようなものでなければならないのか?
第10のヒント
幼女たちはチェス盤の状況を数値化するが、その数値からチェス盤の状況を再現することは原理的に不可能である
「問題のポイント」で述べたことと少し似ています。
ポーンを1つ操作するという行動でしか幼女間の情報の伝達が無い以上、幼女間で確実に共有できるのは「事前の戦略」と「幼女Aが操作した後のチェス盤の状況」のみです。
幼女Bがチェス盤の初期状態を知ることは絶対に不可能です。
つまり、幼女Bが認識できるチェス盤は「操作された後のチェス盤」だけ。
そして幼女Bはそれを数値化する。
ということは?
第11のヒント
幼女Aはチェス盤の状況を数値化し、後に幼女Bがチェス盤を数値化した際にそこから「正解となる整数」を導き出せるようにポーンを操作する
論理的に考えるとこうなります。
問題が解けるのであれば、このような進行にならなければ不自然なのです。
第12のヒント
幼女たちがチェス盤の状況を数値化して得られる数値は、64通り
最終的に幼女Bがチェス盤を見て64通りの整数を読み取らねばならないことから、幼女たちが行う数値化の結果は64通りに絞られねばなりません。
64マス上に最大64個置かれうるポーンの不規則な配置を64通りに集約して数値化する——。
これまでのキーワードから導かれる発想とは。
最後のヒント
0と1
解答準備編
以降は解答編になります。
解答編の章は「解答準備編」「解説編」「正解編」に分かれています。
「解答準備編」となる本章では解答に必要な3つの知識を学んでいきます。
ヒントでも述べた3つの知識を知っているであろう職業の人とは、数学者あるいは情報工学者(IT系の人)です。
二進数
導入
「十進数」というものをご存知ですか?
7, 13, 520など、私たちが普段よく目にしている数字の表記法です。
数字の各桁は十の倍数がいくつあるかを示しており、たとえば520であれば、
102×5 + 101×2 + 100×0
すなわち
100×5 + 10×2 + 1×0 = 520
ということを表します。
「二進数」とは、各桁が二の倍数で構成される数字の表記法です。
111, 1101, 1000001000など、映画やドラマのコンピュータでよく目にするアレです。
数字の各桁は二の倍数がいくつかあるかを示しており、たとえば111であれば
22×1 + 21×1 + 20×1
すなわち
4×1 + 2×1 + 1×1 = 7
ということを表します。
二進数の「111」は、十進数で表すと「7」になるわけです。
二進数を求めよう
さて、この論理クイズでは「十進数と二進数の変換」が必須になります。
「計算が面倒だ!」と思う方は、次の項の「十進数と二進数の対応表」まで読み飛ばしてください。
十進数から二進数への変換
十進数を2で割って、それをさらに2で割って……と、商が0になるまで繰り返し、最後の余りを先頭にして順次並べると、元の数を二進数にした値が求められます。
例:十進数の13を二進数に変換すると?
13 ÷ 2 = 6 余り 1
6 ÷ 2 = 3 余り 0
3 ÷ 2 = 1 余り 1
1 ÷ 2 = 0 余り 1
十進数の13は二進数だと1101
二進数から十進数への変換
元となる二進数を基準に、「各桁の値×位の重み(何の位か)」という計算を行うことで十進数に変換した値が求められます。
例:二進数の1101を十進数に変換すると?
1×23 + 1×22 + 0×21 + 1×20
= 1×8 + 1×4 + 1×0 + 1×1
= 8 + 4 + 0 + 1
= 13
二進数の1101は、十進数だと13
十進数と二進数の対応表
6桁の二進数で表現できる主な数値をまとめました。
何となく雰囲気をつかんでください。
| 十進数 | 二進数 |
| 0 | 000000 |
| 1 | 000001 |
| 2 | 000010 |
| 3 | 000011 |
| 4 | 000100 |
| 5 | 000101 |
| 6 | 000110 |
| 7 | 000111 |
| 8 | 001000 |
| 15 | 001111 |
| 16 | 010000 |
| 31 | 011111 |
| 32 | 100000 |
| 62 | 111110 |
| 63 | 111111 |
パリティ
「パリティ」とは数学・物理学・情報工学等で用いられる概念で、ものすごく乱暴に言うと「合計が偶数か奇数か」ということに着目する発想のことです。
二進数と併用されることが多く、通信の誤りを検出する手法である「パリティチェック」等に使われています。
ビットの合計数が偶数ならその状態を「偶数パリティ」、奇数なら「奇数パリティ」と言ったりします。
言葉自体を覚える必要はありませんが、「合計が偶数か奇数か」という発想がこの論理クイズでは重要になることだけ覚えておいてください。
排他的論理和(XOR)
排他的論理和とは、2つの入力のどちらか片方だけ真の時は結果が真となり、そうでない時は偽となる論理演算です。
真偽を1と0に置き換えて考えると、「どちらか一方が1の時のみ答えが1になり、そうでなければ0になる」演算です。
ちょっとやってみましょう。
真偽を1と0に置き換えた場合、計算結果は以下のようになります。
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0
※⊕は排他的論理和を示す数学記号
「どちらかが1の場合のみ答えが1になる」ことが見てとれますね。
さて、2進数表現した数値の各ビットに対し排他的論理和の計算を行うことを「ビットごとの排他的論理和(XOR演算)」と言います。
ビットごとの排他的論理和には以下の性質があります。
性質1:等しい数値同士で計算を行うと0になる
A⊕A = 0
性質2:同じ数値で計算を2回繰り返せば値は元に戻る
(A⊕B) ⊕ B = A
性質3:複数の数値で計算を行った際の各ビットの結果は以下に等しい
1)1であるビット総数が偶数のとき0
2)1であるビット総数が奇数のとき1
以下はその証明です。
読まなくてもいいです。
とりあえず「どちらかが1の場合のみ答えが1になる」計算があるということだけ覚えておいてください。
性質1:
同じ数値を2進数表現すると各ビットは同一になるので、定義(0⊕0 = 0, 1⊕1 = 0)より自明である。
性質2:
結合法則より、
(A⊕B) ⊕ B
= A ⊕ (B⊕B)
= A ⊕ 0
= A
よって、(A⊕B) ⊕ B = A である。
性質3:
1⊕0=1, 0⊕1=1であるため、連続する複数の排他的論理和の計算において、題意を証明するためには0であるビットを除いて考えてよい。
以上より、前提となる計算式を
f(n) = a1 ⊕ a2 ⊕ ・・・ ⊕ an
とおく。
ビット総数nは2以上の整数である。
また、任意のxについて ax = 1 なので
f(n) = 1 ⊕ 1 ⊕ ・・・ ⊕ 1
である。
(1)ビット総数が偶数である場合
nは2以上の偶数なので、奇数番目と偶数番目の項が1対1の1組になる組み合わせが必ず存在する。
f(n) = (1 ⊕ 1) ⊕ ・・・ ⊕ (1 ⊕ 1)
ビットごとの排他的論理和の計算においてA⊕A=0なので、
f(n) = 0 ⊕ 0 ⊕ ・・・ ⊕ 0
同様に
f(n) = 0
となり、ビット総数が偶数の場合、その排他的論理和は0になる。
(2)ビット総数が奇数である場合
nは3以上の奇数なので、最後の項を除いて、奇数番目と偶数番目の項が1対1の1組になる組み合わせが必ず存在する。
f(n) = (1 ⊕ 1) ⊕ ・・・ ⊕ (1 ⊕ 1) ⊕ 1
(1)より、最後の項以前の計算結果は0になるため
f(n) = 0 ⊕ 1
よって f(n) = 1 となり、ビット総数が奇数の場合、その排他的論理和は1になる。
解説編
ここから順を追って解答のプロセスを考察・解説していきます。
まず考えること
まず始めに、本問の前提を確認しましょう。
悪魔が指定する整数は64通り。
幼女側の回答のチャンスは1回きりなので、当てずっぽうだと1.5%程度の確率でしか正解しません。
しかし本問では、論理クイズであるという特性上100%正解できる解答法があるとすでに知らされています。
つまり、この1.5%の賭けを100%の法則に変える何らかのプロセスが存在するのです。
そうでなければいけません。
情報量の壁を越えろ
この論理クイズにおいて最大の焦点となるのが「幼女Aは幼女Bにどうやって最大64通りの情報を伝えるのか」という問題。
幼女Aにできる行動は、チェス盤の様子を見て、どれかひとつのポーンを操作することだけ。
「どのポーンを操作したか」を伝達する手段はありません。
そのため幼女Aが行えるのは「あるマスのポーンの状況を変えること」のみです。
「ポーンを置く」「ポーンを除く」のどちらか。
マスにはポーンが「置かれている」「存在しない」のいずれかしかありませんから、幼女Aの行為にはマスのポーンを「有から無へ」「無から有へ」の2通りの状態にできる性質があります。
つまり、幼女Aの操作には1ビット(2通り)の情報量があると言えます。
しかし正解の可能性は「1〜64の整数いずれか」という64通り。すなわち6ビット。
ポーンを6つ操作できるのであれば簡単に解決できるのですが、あいにく操作できるポーンは1つのみ。
どうすれば1ビットの変更で6ビットの情報を操れるのでしょうか?
1ビットとは?
いきなり「1ビット」という単語が出てきて驚いた方もいるでしょう。
1ビットとはコンピュータ内部における情報表現の最小単位で、「0」か「1」が格納されます。
言い換えると、1ビットとは0と1の2種類の情報表現が可能であるものです。
つまり2通りを表現できる単位です。
たとえば電球はON/OFFという2つの状態があり、なおかつそれを切り替えられるので、1ビットの情報量があると言えます。
この「ビット」という単位が本問では重要になります。
そこで、チェス盤が2マスの場合を考えて「1ビットの威力」を見てみましょう。
チェス盤が2マスの場合を考えよう
問題
マスが2つしかないチェス盤があります。
幼女Aは部屋に入り、悪魔がランダムにポーンを置いたチェス盤を見ます。
悪魔は幼女に1~2の整数のどちらかを告げ、その後幼女Aは「いずれかのマスにポーンを置く」「いずれかのマスのポーンを取り除く」のどちらかの操作を1回だけ行います。
幼女Aは部屋から出ます。
幼女Bは部屋に入り、チェス盤の様子を見て幼女Aに告げられた整数を当てます。
この時、幼女たちはどのような戦略を取るべきでしょう?
解答
2つのマスをそれぞれ「1マス目」「2マス目」とします。
悪魔が告げる整数は以下の2通りです。
(1)、(2)
悪魔が作りうるチェス盤のポーンの状態は以下の4通りです。
(○,○)、(○,×)、(×,○)、(×,×)
※左側が「1マス目」、右側が「2マス目」
※ポーンの有る無しをそれぞれ「○」「×」という記号で表現しています
幼女たちは、「正解が1なら1マス目を○にする」「正解が2なら1マス目を×にする」という戦略を事前に共有しておきます。
幼女Aは、チェス盤の初期状態に応じて以下のいずれかの操作を行います。
悪魔が幼女Aに告げたのが1の場合:
初期状態が(○,○)であれば、2マス目のポーンを除き(○,×)にする
初期状態が(○,×)であれば、2マス目にポーンを加え(○,○)にする
初期状態が(×,○)であれば、1マス目にポーンを加え(○,○)にする
初期状態が(×,×)であれば、1マス目にポーンを加え(○,×)にする
悪魔が幼女Aに告げたのが2の場合:
初期状態が(○,○)であれば、1マス目のポーンを除き(×,○)にする
初期状態が(○,×)であれば、1マス目のポーンを除き(×,×)にする
初期状態が(×,○)であれば、2マス目のポーンを除き(×,×)にする
初期状態が(×,×)であれば、2マス目にポーンを加え(×,○)にする
幼女Bは、チェス盤の1マス目が○なら「1」、×なら「2」と答える。
1ビットと6ビット
いかがでしょう。
2マス2整数という縛りではありますが、1度きりの操作で4通りの状況を任意の2通りに変更することができました。
ポーンを1つ操作することで、1ビットすなわち21=2通りの表現が可能でした。
もしポーンが6つ操作できるなら、6ビットすなわち26=64通りの表現が可能になりますが、これは前提から外れてしまいます。
とにかく何かうまいこと「ポーン1つの操作」に6ビット分の情報量を与えねばなりません。
チェス盤という存在
ところで、この問題において「ポーンがランダムに置かれたチェス盤」とは何を意味するのでしょう?
チェス盤のマスは64通り。
表現すべき数も64通り。
ポーンの配置方法は膨大。
この問題に答えがあるとするなら、「ポーンがランダムに置かれた64マスのチェス盤の状況を、6ビット分すなわち64通りに圧縮する方法」があるはずです。
幼女Bはチェス盤を見て1~64の数を読み取らねばならないのですから、当然、あらゆるチェス盤の状況は最終的に64通りのいずれかにならねばなりません。
そうでなければ問題が成立しないのです。
チェス盤に数字を割り振る
この問題は、幼女Aがチェス盤の初期状態を数値化することから全てがスタートします。
それに先立って必要なのが、「チェス盤のマスに0~63の番号を割り振る」こと。
ここではひとまず、盤の左上から右に向かって規則的に0,1,2,3…と割り振り、盤の右下端に63という番号が割り振られたことにします。
なお視認性向上のため、チェス盤の黒白模様は省略しております。
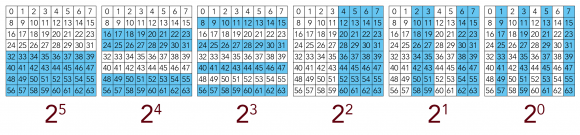
フィルタでチェス盤を色分けする
チェス盤を2つに分割して、64マスを2つの領域に分けていきます。
分割パターンは全部で6つ。
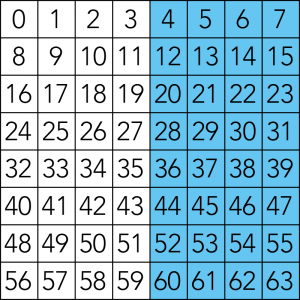
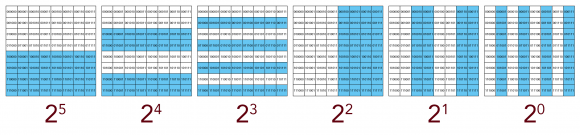
「マスの数字を二進数にした時1が登場する桁」に基づく6つのフィルタを用意します。
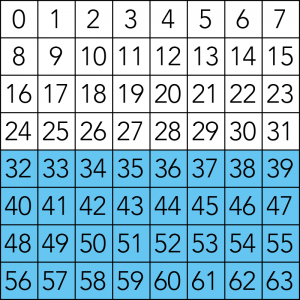
25フィルタ
マスの数字を二進数にした時、25の位に「1」が登場する数字の集合。
該当する数字は32〜63。計32個。
これらは二進数で表すと「100000」〜「111111」となり、必ず25の位(右から6桁目)に必ず1が存在します。
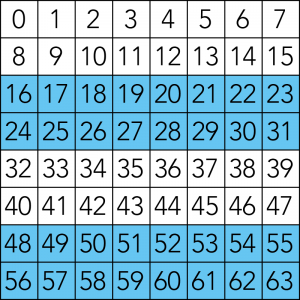
24フィルタ
マスの数字を二進数にした時、24の位に「1」が登場する数字の集合。
該当する数字は16〜31、48〜63。計32個。
これらは二進数で表すと「010000」〜「011111」、「110000」〜「111111」となり、必ず24の位(右から5桁目)に必ず1が存在します。
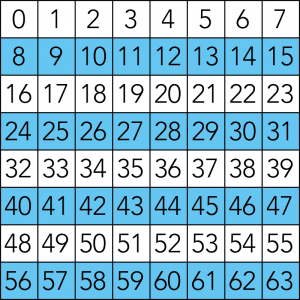
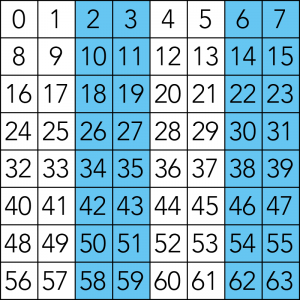
23フィルタ
マスの数字を二進数にした時、23の位に「1」が登場する数字の集合。
該当する数字は8〜15、24〜31、40〜47、56〜63。計32個。
これらは二進数で表すと「001000」〜「001111」、「011000」〜「011111」、「101000」〜「101111」、「111000」〜「111111」となり、必ず23の位(右から4桁目)に必ず1が存在します。
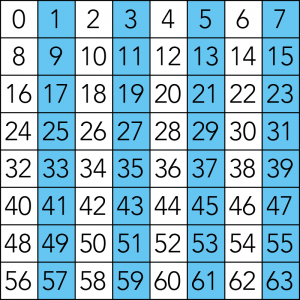
22フィルタ
マスの数字を二進数にした時、22の位に「1」が登場する数字の集合。
該当する数字は全部で32個。
これらは二進数で表すと「000100」〜「000111」(以下略)となり、必ず22の位(右から3桁目)に必ず1が存在します。
21フィルタ
マスの数字を二進数にした時、21の位に「1」が登場する数字の集合。
該当する数字は全部で32個。
これらは二進数で表すと「000010」〜「000011」(以下略)となり、必ず21の位(右から2桁目)に必ず1が存在します。
20フィルタ
マスの数字を二進数にした時、21の位に「1」が登場する数字の集合。
該当する数字は全部で32個。
これらは二進数で表すと「000001」、「000011」(以下略)となり、必ず21の位(右から1桁目)に必ず1が存在します。
6つのフィルタ一覧
以上のフィルタを一列に並べたものがこちらです。
そして、実際に二進数に変換したものがこちら。
画像を拡大してみると、それぞれのフィルタが示す位に「1」が存在するものが青く塗られていますね。
フィルタの性質
ご覧のように、各フィルタによって分割された領域は、そのフィルタが示す2の階乗の位にて1が存在するものの集合体です。
たとえばチェス盤右上に登場する十進数の「7」は二進数では「000111」ですが、このとき二進数で「1」が登場するのは右から3桁目、2桁目、1桁目——すなわち22の位、21の位、20の位です。
これらの位に「1」が存在するので、
25×0 + 24×0 + 23×0 + 22×1 + 21×1 + 20×1
= 0 + 0 + 0 + 4 + 2 + 1
= 7
となり、二進数「000111」は十進数で「7」になるわけです。
当然ですね。
フィルタを用いるともう少し話が簡単になります。
たとえば「40」のマスをご覧ください。
「40」のマスが青に塗られているフィルタはどれでしょう?
25フィルタと23フィルタですね。
これはつまり、十進数の「40」は二進数に変換すると25の位と23の位に1が存在する「101000」という数値になることになります。
実際に計算してみると、
40 ÷ 2 = 20 余り 0
20 ÷ 2 = 10 余り 0
10 ÷ 2 = 5 余り 0
5 ÷ 2 = 2 余り 1
2 ÷ 2 = 1 余り 0
1 ÷ 2 = 0 余り 1
十進数の40は二進数だと101000
101000
25×1 + 23×1
= 32×1 + 8×1
= 40
当然ですね。
フィルタの特徴
さて、これらのフィルタを活用すれば64個のあらゆる整数を二進数で表現できます。
ここで重要なのが、マスに書かれた0から63までの整数を表現する時、どれひとつとして同じフィルタの組み合わせを要する数字はないということです。
ある数を選んだとき、二進数でその数を作るのに必要なフィルタの組み合わせはすべて異なる、とも言えます。
そしてフィルタは6枚なので、フィルタの組み合わせ方は26=64通り。
すなわち、マスに書かれた0から63までの64個の数字を表現する時、6枚のフィルタの組み合わせ64通りが全て網羅される。
パリティによる数値化
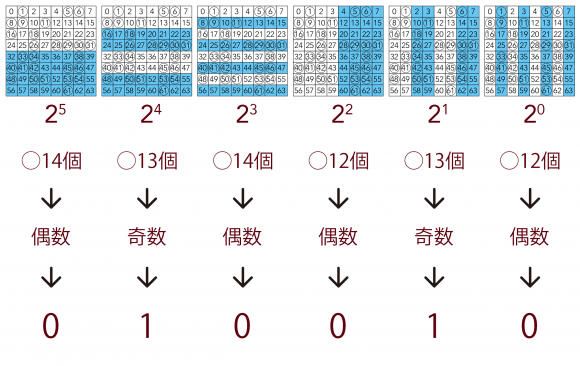
幼女がチェス盤の状況を数値化する方法。
それは、「各フィルタの領域内のマスにポーンが置かれた総数」が「偶数パリティ」か「奇数パリティ」をチェックし、前者なら0、後者なら1とし、その結果を二進数と見なすというもの。
意味不明ですね!
詳しく解説していきます。
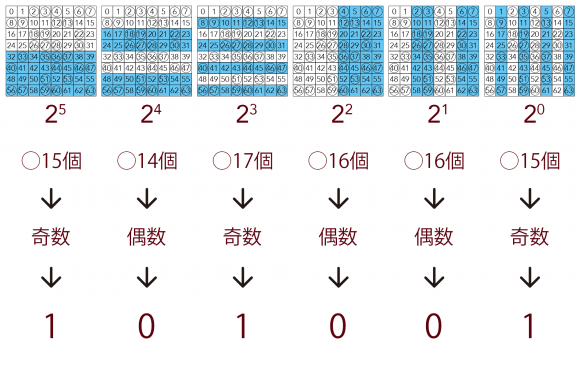
初期状態におけるチェス盤が以下の様子であると仮定します。
※○がついているマスにポーンが置いてあります
各フィルタごとの領域内にいくつ○があるかを数え上げます。
◯の総数が偶数なら、そのフィルタにおいて偶数パリティであるため結果は0。
◯の総数が奇数なら、そのフィルタにおいて奇数パリティであるため結果は1。
これらの結果をメモしておきます。
そうして出てきた0と1を前から順番に羅列していくと、6桁の0と1が並びます。
上の図でいうと「101001」ですね。
この数字の羅列こそが初期状態のチェス盤を数値化したものになります。
つまり、この例で言うと「101001」を十進数に直した「41」こそが初期状態のチェス盤の数値です。
何が起こったのか
「チェス盤を(ある方法で)色分けした領域内に存在するポーンの総数が偶数か奇数か」。
この作業で行っているのはそれだけです。
ひとつでもポーンの位置がズレれば「101001」という数値にはなりませんし、そもそも「101001」になるポーンの配置方法はこれ以外にも星の数ほどあります。
重要なのは、この一連の作業で「101001」という6桁の数値を得られたということ。
そしてその数字は二進数と見なせること。
さらに言うと、この一連の作業で得られる可能性がある数値は「000000」から「111111」の64個で、そして幼女Aがチェス盤上に表現する数も、幼女Bがチェス盤上から読み取るべき数も、いずれも64個のいずれかであるということ。
最後に、幼女Aのたった1回の操作で6つのフィルタのパリティは自由自在に変更できること。
最初に、チェス盤の左上を基準にして、そこから規則的に0から63までの数字をのマスに割り振りました。
次に、それを二進数にしたときの値に基づいて6つのフィルタを作成しました。
そして、このフィルタを用いれば、0から63のあらゆる数字が表現できました。
最後に、フィルタの領域に存在するポーンの数が偶数か奇数かを調べ、偶数なら0、奇数なら1として、並べて二進数に見なしました。
この最後のプロセスに注目してください。
やったことは、たまたま得られた「101001」という数値を「これは二進数だ」と見なしただけ。
そこに必然性のようなものはありません。
特別な意味もありませんし、今回「101001」が得られたのは偶然です。
チェス盤に割り振り始める数字を右上基準にしていたら、得られる数値は全く別のものになってしまいます。
核心へ
大切なのは——そしてこの論理クイズにおいてもっとも大きな意味を持つのは——この一連のプロセスを経ることによって、あらゆる初期状態のチェス盤のポーンの配置から、たったひとつの二進数の数値が見出せるということ。
そして、この数値が「各フィルタの領域内のポーンが偶数か奇数か」に基づいて得られている以上、たったひとつポーンを増減するだけで、チェス盤の状況を示す二進数を「000000」〜「111111」の64通りすべてに変更できるということ。
さあ、いよいよ大詰めです!
少し前にフィルタについて述べた時のことを思い出してください。
6枚のフィルタにはどんな特徴がありましたか?
「マスに書かれた0から63までの整数を表現する時、どれひとつとして同じフィルタの組み合わせを要する数字はない」。
それから?
「ある数を選んだとき、二進数でその数を作るのに必要なフィルタの組み合わせはすべて異なる」。
「マスに書かれた0から63までの64個の数字を表現する時、6枚のフィルタの組み合わせ64通りが全て網羅される」
ここ! これです!
チェス盤上に存在する0〜63までの数字のすべての数が、異なる組み合わせのフィルタによって塗り分けられていました。
そしてその全ての組み合わせは、0〜63までの数字に対応していました。
もうお分かりですね?
チェス盤を数値化した二進数は、各フィルタの領域内に存在するポーンの総数が「偶数」か「奇数」かによって決まります。
偶数に1を加えたら奇数に、奇数に1を加えたら偶数になります。
偶数から1を引いたら奇数に、奇数から1を引いたら偶数になります。
チェス盤上に存在する0〜63までの数字は、フィルタの組み合わせ64通り全てを網羅する。
つまり、それぞれの領域内のポーンの数を1つ増やすか1つ減らすかだけで、チェス盤を数値化した二進数を「000000」〜「111111」のどれでも好きなように変えることができるのです。
具体例を見てみましょう!
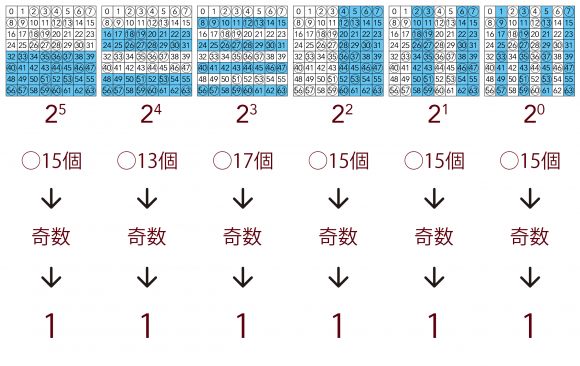
上の方で挙げた例です。
これに一連のプロセスを当てはめると「101001」すなわち十進数で「41」という数値が得られました。
この状態で、どこかのマスに1つポーンを置く、あるいは1つ取り除く、それだけでこのチェス盤を数値化した数値を「000000」〜「111111」(十進数「0」〜「63」)のどれでも好きな数値に変えられる。
それがこれまでの結論です。
たとえば……十進数で「63」を示す「111111」にしたい場合は?
「101001」を「111111」にするには、25、23、20の位はそのままで、24、22、21の位を「1」にする必要があります。
つまり、25、23、20のフィルタのポーン合計数はそのままで、24、22、21のフィルタのポーン合計数を奇数にする必要があります。
すなわち、「010110」の二進数があるマスにポーンを追加あるいは取り除けばいいわけです。
「010110」は十進数に直すと「22」。
22のマスにあるポーンを操作すればそれで終わりです。
22のマスにはすでにポーンがあるので、取り除いてみましょう。
さあ、これで本当に望む数値になったのでしょうか。
再度数値化して確認してみます。
得られた値は「111111」。
見事に十進数の「63」になっています!
このようなプロセスを辿ることで、あらゆる初期状態のチェス盤は64通りに数値化され、どこかひとつのマスの状況を変えるだけで、64通りの数値にすることが可能になるのです!
ポーン操作についての重要な疑問
チェス盤の数値を変えたくない場合は?
幼女Aには、どこかのマスに「ポーンを置く」「ポーンを取り除く」のいずれかの行動を必ず実行しなければならないという制約がありました。
もし、初期状態のチェス盤を数値化した数値を変えたくない場合はどうすればよいのでしょう?
簡単です。
その時は、「000000」——十進数の「0」に当たるチェス盤左上のマスのポーンの状態を変えればいいのです。
確認してみてください。
チェス盤左上に割り振られた「0」というマスは、いかなるフィルタの領域でもありません。
このマスだけは、ポーンを置いても取り除いても、各フィルタの領域のポーンの総数は全く変わりません。
つまり、左上の「0」というマスには、ポーンが有ろうが無かろうがチェス盤全体の数値は変わらないという性質があります。
なので、最初にチェス盤を数値化した後、その数値を変えたくなければ、盤左上の「0」のマスにポーン置くか取り除くかすればいいのです。
ポーンを置きたいマスに既にポーンがあった場合は?
ポーンを加え、あるいは取り去ることであらゆる数値を表現できることが判明しました。
では、ポーンを置きたいマスに既にポーンが置かれていた場合は?
あるいは、ポーンを取り除きたいマスにそもそもポーンが無い場合は?
これに対する答えは、この論理クイズの本質に深く関わる内容です。
簡潔に答えを述べるとこうなります。
「あるマスにポーンを置く/取り除くという行動は、いずれもマスのポーンの数を必ず増減させるため、この問題においては本質的に同じである」。
思い出してください。
幼女Aがポーンを操作するのは、チェス盤の状況を思いのままに変えるためでした。
そのために必要なのは「たった1箇所のマスにポーンを加えたり減らしたりすること」でした。
さて、ここからが重要です。
「たった1マスのポーンの数を増減させること」がなぜ大事かというと、「ある領域内のポーンの総数が偶数か奇数か」によってチェス盤数値化の結果が決まるからでした。
「ポーンの総数」は必ず偶数か奇数になります。
偶数に+1されれば奇数になり、-1されても奇数になります。
奇数に+1されれば偶数になり、-1されても偶数になります。
偶数と奇数は1が増減されれば必ず偶奇が入れ替わります。
「ポーンの総数」は偶数か奇数かしかありえません。
「あるマスにポーンを置きたい」というのは「そのマスの偶奇を入れ替えたい」ということです。
「ポーンを置きたいのに既にポーンがある状態」というのは、「そのマスの偶奇を入れ替えたい状態でなおかつマスには既にポーンがある状態」です。
例外となる「000000」のマスを除いて考えると、ポーンがある状態のマスの偶奇を入れ替えるためにはポーンを+1もしくは-1すればどちらにしても必ず偶奇は入れ替わることになります。
ポーンが有るマスにポーンを+1するのはルール上できません。なので-1するしかないのですが、結果は同じです。
ポーンが無いマスからポーンを-1したい場合も同様です。
以上より、「あるマスにポーンを加える」「あるマスからポーンを取り除く」という操作を必ずどちらか1回だけ行わなければならない幼女Aに課されたルールの本当の意味は、彼女にどんな状態のマスでもたった1回でそのマスの偶奇を入れ替えることを可能にさせることだと言えます。
あまりにも強力な制約に思えたルールには、きちんと問題を解決するためのロジックが組み込まれていたわけですね。
よりシンプルな方法——排他的論理和
※発展的な内容になります。ここは読まなくても大丈夫です
以上長々と「チェス盤を数値化しポーンを操作すべきマスを求める方法」について述べてきましたが、もっとシンプルな(そして本質的な)やり方が存在します。
XOR(排他的論理和)演算を使う方法です。
2の階乗フィルタ6枚を使う、偶数パリティか奇数パリティかを0と1に変換する、二進数を自在に操るために領域内の偶奇を操作する。
これらの過程において使われた計算には、すべてXOR演算が絡んでいます。
順を追って見ていきましょう。
チェス盤を数値化する
まずチェス盤の状況を数値化するプロセスですが、計算的には「ポーンがあるマスの数字をすべて抜き出して二進数変換しそれらすべてについてXOR演算を行う」の一言で事足ります。
というか、長々と述べてきたのはこれを視覚的に表現するためであって、やりたいことは最終的にこれでした。
ビットごとのXOR演算の性質に「複数の数値で計算を行った際の各ビットの結果は、1であるビット総数が偶数のとき0、1であるビット総数が奇数のとき1にある」というものがありました。
この性質を活用して上記の計算をよく考えてみると、フィルタや偶数奇数パリティを使ったチェス盤の数値化計算と全く同じ計算過程を辿ることになります。
そうです。排他的論理和を使えば一瞬でカタがつくのです。
ポーンを操作すべきマスを求める
チェス盤を数値化した値を別のものに変えたい時も、XOR演算が役立ちます。
数値化したチェス盤の値は「ポーンがあるマスの数字を二進数変換してすべてにXOR演算を行った結果」でしたから、それを別の値にしたいなら、その値と目的になる数値とでXOR演算を行えば操作すべきポーンの位置の二進数が取り出せます。
「101001」を「111111」にしたいのなら、
101001 ⊕ 111111 = 010110
つまり「010110」、十進数で「22」となる位置にあるポーンを操作すべきだと分かります。
これも、計算的にはこれまで述べてきたことと全く同じです。
その他
その他、「マスにポーンを加えたいのに既にポーンが置かれていたらどうするか」みたいなことも全て排他的論理和で説明できます。
「ビットごとの排他的論理和は2の冪を位数とする有限体GF(2n)(※nは自然数)での加減算となりこの体において加算と減算は等しくなる」という性質を理解すれば一発です。
もう全部XORでいいのでは?
その通りです。
排他的論理和を使えば、この論理クイズでやるべきことは3行でまとめられます。
しかし、ただそれだけでは「なぜそうなるのか」が分かりづらくなるため、このような迂遠な解説となりました。
最後の解説
ここまで読み進めてくださった方の脳内からは問題文が忘却の彼方に吹き飛んでいる可能性が大なので最後にひとつだけ注意点を述べさせてください。
幼女Aと幼女Bがチェス盤から読み取れる数字は0〜63ですが、最終的に幼女Bが悪魔に答えるべき数字は1〜64の整数です。
どうすればよいのでしょう?
簡単です。
チェス盤の数値化の結果を1つシフトさせればいいのです。
例えば正解が14である場合、幼女Aはチェス盤を数値化し、14から1を引いた13をチェス盤に表現します。
そして幼女Bは、チェス盤から読み取った13に1を足した14を悪魔に答えれば正解です。
正解編
実際の解答手順を辿りながら正解を見ていきます。
0.前提
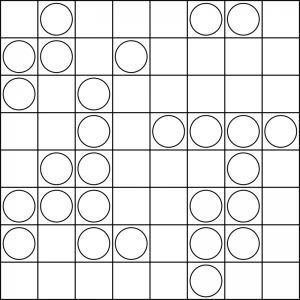
悪魔が告げる整数は53であるとする。
また、悪魔が設定するチェス盤の初期状態は以下であるとする。(◯の場所にポーン)
1.幼女Aはチェス盤に0から63の番号を割り振る
悪魔から正解となる整数53を告げられた幼女Aは、事前の打ち合わせ通りにチェス盤の64マスに0〜63の数字を割り振っていく。
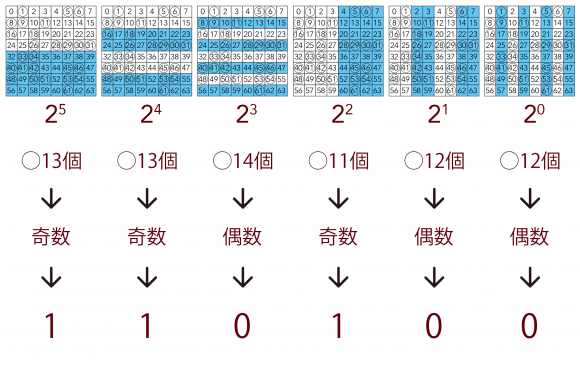
2.幼女Aはチェス盤の状況を数値化する
幼女Aはフィルタを活用(あるいはポーンがあるマス数字すべての排他的論理和を計算)し、チェス盤を数値化した「010010」という二進数を得る。
3.幼女Aはどのポーンを操作すべきか計算する
悪魔が告げた整数53から1をマイナスした52という数字をチェス盤に表現しなければならない。
52は二進数に変換すると「110100」。
フィルタを活用(あるいは現在の数値と求める数値とで排他的論理和を計算)し、操作すべきポーンのマスは「100110」すなわち「38」であると算出する。
「38」のマスには既にポーンがあるので、幼女Aはそのポーンを取り除く。
4.幼女Bはチェス盤の状況を数値化する
幼女Aと入れ替わりで部屋に入った幼女Bは、現在のチェス盤を幼女Aと同じプロセスで数値化する。
チェス盤から読み取れる二進数は「110100」。
十進数に変換すると「52」。
5.幼女Bは悪魔に正解を告げる
最後に、幼女Bはチェス盤から読み取った十進数「52」に+1した数「53」を正解数として悪魔に告げる。
6.悪魔はニッコリする
おしまい
最後に
ここまでお読みいただきありがとうございました。
この論理クイズが、殺伐とした現代社会における一抹の清涼剤となりますように。
参考サイト
さまざまな論理パズルをまとめていらっしゃるcatupperという方のGist(ソースコード共有サービス)。
本論理クイズは、こちらの11番目のテキストファイル「11.2人の幼女とチェス盤の部屋」から問題文の要旨を引用いたしました。
問題を見つけたまではよかったのですが、あまり知られていない問題なためか日本語での解答が見つかりませんでした。
英語で検索したところ、「DataGenetics」というブログの「Impossible Escape?(脱出不可能?)」という記事に書かれた論理クイズの内容が本問とかなり似ていました。
当記事の解説は、この「DataGenetics」の記事内の解説を参考にしています。
なお「Impossible Escape?」に書かれている論理クイズ(看守と2人の囚人)は、「最初に告げられるのが1〜64の整数ではない」「ポーンではなくコインが使われている」等の細かな違いがあり、初見での見た目上の難易度はそちらの方がやや高くなっています。(本質的には同じ問題ですが)
当記事作成用にものすごくいい加減に意訳した文章を記事化しましたので、ご参考までにどうぞ。
「Impossible Escape?」意訳記事「論理クイズ「2人の囚人とチェス盤」解説英文の意訳」
Yet another prisoner puzzle
雰囲気だけ参考にしました。
140字以内の問題文
悪魔は8×8のチェス盤にランダムにポーン(0〜64個)を置き、どこかのマスを指定する。幼女Aはそれを見てどこか1マスに対し「ポーンを置く」「取り除く」のいずれかの行動を1回のみ行う。その後、幼女Bはチェス盤の様子を見て悪魔がどのマスを指定したのか答えねばならない。どうすればいい?