必要なのは、ヒラメキと思考能力。
この問題が解けますか?
今回ご紹介するのは、ネットで有名な論理クイズ「23人の幼女と石像の部屋」。
解答不可能に思えるこの問題には、おどろくほどスマートな答えが隠されています。
事前知識は必要ありません。
発想力がすべてのカギを握ります。
問題
23人の幼女が、ある館に閉じ込められた。
この館には「石像の部屋」がある。
「石像の部屋」には石像が置いてあり、東西南北のいずれかを向いている。
幼女たちはそれぞれ個室に閉じ込められており、互いに連絡を取り合うことはできない。
悪魔は幼女を1人ランダムに選んで、石像の部屋につれてくる。
誰がいつ選ばれたかを他の幼女は知ることができない。
石像の部屋につれてこられた幼女は、以下の行動をどれかを必ず実行しなければならない。
- 1. 石像を左に90度回転させる
- 2. 石像を右に90度回転させる
- 3. 石像を壊す
幼女が石像を回転させた場合、その幼女は個室に戻され、次にランダムに選ばれた幼女が石像の部屋につれてこられ、同様の操作をする(以下繰り返し)。
幼女が石像を壊した場合、石像の部屋に一度でも入ったことのある幼女全員が解放される。
23人全員の幼女が確実に解放されるには、どのような戦略を取ればよいか?
幼女たちは、ルールを知った上で開始前に戦略を練ることができる。
幼女が石像の部屋に呼び出されるタイミングだが、同じ幼女が連続して呼び出されることもある。
ただし、どの幼女も充分な時間を待てば必ず何度でも呼び出されるものとする。
しかし、「充分な時間」がどれほどの時間なのかは分からない。
また、幼女たちは石像の最初の向きを知らない。
さあ、解いてみよう!
これは非常に洗練された問題です。
数学的な知識は必要ありません。
とてもエレガントな解答が存在するので、ぜひ時間を使って考えてみてください。
解けた時、あるいは解答を知った時、きっと爽快感に満ちあふれるはずです。
以下は「重要なポイント」「ヒント」「解答」「解説」という順で章が進みます。
自力で解きたい方は「重要なポイント」だけ読んでください。
重要なポイント
幼女たちの目的
幼女が石像を壊した場合、石像の部屋に一度でも入ったことのある幼女全員が解放される。
幼女たちの目的は、23人全員が解放されること。
そのためには、「石像の部屋に23人全員が入ったことがある」と確信した幼女が石像を破壊しなければなりません。
幼女たちの特徴
幼女たちはそれぞれ個室に閉じ込められており、互いに連絡を取り合うことはできない。
悪魔は幼女を1人ランダムに選んで、石像の部屋につれてくる。
誰がいつ選ばれたかを他の幼女は知ることができない。幼女たちは、ルールを知った上で開始前に戦略を練ることができる。
いったんスタートしてしまうと、幼女たちは互いに連絡が取れません。
解放されるためには、「自分は石像の部屋に入ったことがある」と他の幼女に伝えなければいけません。
情報を伝達できる場所はただひとつ。
石像の部屋です。
石像の部屋の特徴
石像の部屋につれてこられた幼女は、以下の行動をどれかを必ず実行しなければならない。
- 1. 石像を左に90度回転させる
- 2. 石像を右に90度回転させる
- 3. 石像を壊す
「石像の部屋」には石像が置いてあり、東西南北のいずれかを向いている。
幼女たちは石像の最初の向きを知らない。
この問題でもっとも重要になるのは、タイトルにもある「石像の部屋」の特徴。
幼女たちは、東西南北いずれかに向いている石像を、「90度回転させる」か「破壊する」のどちらかを必ず行う必要があります。
これによって何とか幼女たちは情報を伝えられそうな気がします。
……と言いたいのですが、「幼女たちは石像の最初の向きを知らない」という強烈なルールが立ちはだかります。
この「石像の初期方向が不明」という制約は、きわめて大きな意味を持ちます。
最後の最後まで頭を悩ませる厄介な要素なのです。
幼女の呼び出し
幼女が石像の部屋に呼び出されるタイミングだが、同じ幼女が連続して呼び出されることもある。
ただし、どの幼女も充分な時間を待てば必ず何度でも呼び出されるものとする。
しかし、「充分な時間」がどれほどの時間なのかは分からない。23人全員の幼女が確実に解放されるには、どのような戦略を取ればよいか?
どの幼女も、充分な時間が過ぎれば確実に石像の部屋に入れます。
ならば、「1ヶ月くらい待って石像を破壊すればいいのではないか?」と思うかもしれません。
しかし、1ヶ月の間で呼び出された幼女は4人だけ、という事態もありえます。
時間経過で判断するのではなく、石像の部屋での行動で、確実に23人全員がこの部屋に入ったことがあると判断しなければなりません。
ヒント
以下ではヒントを述べていきます。
最初は軽いものから、徐々に問題の核心に近くものに変わっていきます。
「ヒント」なので、これらを読んでも確実に解答が可能になるわけではありません。
ヒントを追いつつ、問題にチャレンジしてみてください。
第1のヒント
解答は3つのプロセスで構成される。
解答は、大きく分けて3つのプロセスに分かれています。
それぞれのプロセスで問われるのは発想力。
最後のプロセスではそれに加え、問題の罠を見抜いた着眼点が必要になります。
第2のヒント
石像の「向き」は4種類だが、石像の「状態」はもっと少ない。
1つ目のプロセスに関係します。
東西南北の4方向を向く石像は、そのままでは扱いが難しくなります。
もう少し、石像の状態をしぼりこむことはできないでしょうか?
第3のヒント
幼女たちは役割分担をする。
2つ目のプロセスに関係します。
幼女たちの行動は、全員一緒ではないのです。
※これより先は核心的なヒントになります。
第4のヒント
最初に、幼女たちは「石像破壊役」の1人と「それ以外」の22人で役割分担をする。
2つ目のプロセスの概要です。
まずここに至れるかどうかが最初の関門です。
「石像破壊役の幼女」と「それ以外の幼女」は、全く異なる行動をとります。
第5のヒント
「石像の向き」4通りは、「石像の状態」2通りに集約できる。
そして、石像によって伝えられる情報も2通りのみである。
石像の向きをある2グループに分けて考えることで、石像の状態を2通りに区分できます。
この「2つの状態」を活用することで、幼女たちは過不足ない情報伝達が可能になります。
第6のヒント
石像破壊役の幼女は、カウントを行う。
この問題でもっとも多くの動作を行うのは「石像破壊役の幼女」。
彼女は石像の部屋で何かをカウントしていきます。
※これより先は超核心的なヒントになります。
第7のヒント
石像破壊役の幼女は、カウントが「ある回数」に達した時、石像を破壊する。
この問題を本質を貫くヒントです。
ですが、これだけでは正解になりません。
最後の罠にハマらずに切り抜けられるでしょうか?
第8のヒント
「ある回数」とは、23回ではない。
第9のヒント
「ある回数」とは、22回でもない。
第10のヒント
幼女たちは、確実だがかなり地道な戦略を取る。
最後のヒント
複数回、石像の部屋に入る幼女がいる。
また、場合によっては1回しか石像の部屋に入れない幼女がいる。
解答
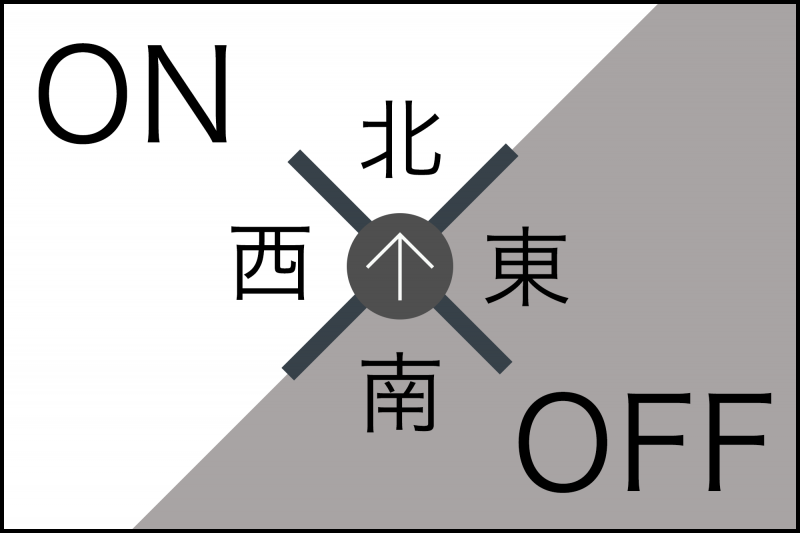
石像の向きを2種類に分割し、「東と南」をOFF、「北と西」をONとする。
石像を破壊する幼女1人を「破壊役の幼女」、それ以外の幼女22人を「通常の幼女」とする。
通常の幼女たちは、石像の部屋に入った時、次の行動を行う。
1. 石像の状態が「ON」なら、そのままにする
2. 石像の状態が「OFF」なら、「ON」にする(2回まで)
3. 石像の状態が「OFF」であるのが3回目以降だった場合、そのままにする
石像破壊役の少女は、石像の部屋に入った時、次の行動を行う。
1. 石像の状態が「ON」なら、「OFF」にする。石像の状態が「ON」になった累計回数をカウントしておく
2. 石像の状態が「OFF」なら、そのままにする
3. 石像の状態が「ON」であるのが44回目の時に石像を破壊する。
幼女たちは23人全員解放される。
解説
「ああなるほどね」みたいな感じで解答を読んだものの、いきなり「44回目」という何の脈絡もない数字が出てきて驚いた方も多いでしょう。
22回でも23回でもなく、44回という不可解な数。
この数字こそが、本問を象徴する最大の難関にして最後の答えです。
以下では解答を詳しく解説していきます。
1. 石像を二値で考える
石像の向きを2種類に分割し、「東と南」をOFF、「北と西」をONとする。
石像の向きを「東西南北」で考えるのではなく、「2つの値」で考えます。
図にするとこんな感じです。
ここで重要なのは、石像の状態をON/OFFの2つに限定することにより、幼女たちは1回の石像の操作で
「ON/OFFを切り替える」
「ON/OFFを切り替えない」
のどちらも確実に行える、ということです。
たとえば石像が南を向いていた時、「ONに切り替える場合」は左に90度、「OFFのままにする場合」は右に90度回転させればいいわけです。
2. 幼女たちの役割分担
石像を破壊する幼女1人を「破壊役の幼女」、それ以外の幼女22人を「通常の幼女」とする。
まず、23人の幼女を2つのグループに分けます。
「通常の幼女」22人の役割は、「石像の部屋に来たことがあると伝える」こと。
「石像破壊役の幼女」1人の役割は、「誰かが石像の部屋に来たことを確認してその回数をカウントし、最後に石像を破壊する」こと。
おおざっぱに言うとこんな感じです。
3. 具体的な手順
通常の幼女たちは、石像の部屋に入った時、次の行動を行う。
1. 石像の状態が「ON」なら、そのままにする
2. 石像の状態が「OFF」なら、「ON」にする(2回まで)
3. 石像の状態が「OFF」であるのが3回目以降だった場合、そのままにする石像破壊役の少女は、石像の部屋に入った時、次の行動を行う。
1. 石像の状態が「ON」なら、「OFF」にする。石像の状態が「ON」だった累計回数をカウントしておく
2. 石像の状態が「OFF」なら、そのままにする
3. 石像の状態が「ON」であるのが44回目の時に石像を破壊する。
実際の進行を確認しながら考えていきましょう。
石像の状態「ON」は、「私はここに来て石像を動かした」というメッセージを意味します。
通常の幼女たちは、石像の状態が「OFF」なら「ON」に切り替えます。
これにより、他の幼女たちに「石像を動かした幼女がいる」という事実を伝えます。
幼女たちが部屋に入った時、石像が「ON」ならば「誰かがこの部屋に入った」ということが確実にメッセージとして残されているため、それを保存すべく石像の状態を「ON」のままで保持します。
次に石像破壊役の幼女が石像の部屋に入った時、石像が「ON」なら、彼女は「少なくとも自分以前に誰か1人がこの部屋を訪れた」ことが分かります。
彼女はカウントを+1し、石像をONからOFFにリセットすることで、再び誰かがONにしてくれるのを待ちます。
これを繰り返すことで、最終的に「全ての幼女が確実に石像の部屋を訪れたことがある」と判断した時点で破壊役の幼女は石像を破壊します。
4. 回数の謎
石像の状態が「ON」であるのが44回目の時に石像を破壊する。
いよいよ大詰めです。
これまでの手順を実行することで、幼女たちは館からの脱出が可能になります。
しかしここで当然の疑問が浮かび上がります。
なぜ通常の幼女たちは「OFF」から「ON」への切り替えを2回まで実行するのか?
なぜ破壊役の幼女は「ON」になっている回数が44回目になるまで待つのか?
22回ではダメなのか?
シンプルで––なおかつ上手くいきそうな––場合を考えてみましょう。
通常の幼女たちは、自分が石像の部屋に入り、石像がOFFだったら初回のみONに切り替える。
それ以外はON/OFFを切り替えない。破壊役の幼女は、石像がOFFならばOFFのままにし、ONならばOFFに切り替える。
石像がONになった回数が22回目のときに石像を破壊する。
とてもシンプルです。
なぜこれではダメなのでしょう?
実は、石像の初期状態が関係しています。
思い出してください。
開始時に石像がどの方向を向いているかは分かりません。
もし石像が最初からOFFの方向を向いているなら、上記の戦略で22回目に石像を破壊すれば23人が解放されます。
しかし、もし石像が最初からONの方向を向いていたら、1番目に呼ばれたのが破壊役の幼女だった場合、彼女は「自分以前に誰か一人が訪れた」と勘違いして+1余分にカウントしてしまいます。
この場合、22回目で石像を破壊してしまうと、脱出できるのは22人のみになってしまう可能性が出てくるのです。
23回ではダメなのか?
ならば、石像があらかじめONだった場合を考えて、ON/OFFの切り替えを1回だけ行うことにして、23回目で石像を破壊するのはどうでしょう?
これも無理です。
もし石像の初期状態がOFFだった場合、通常の幼女たち22人が1回ずつON/OFFを切り替えたら、23回目は永遠にやってこないことになります。
44回目の真実
石像の初期状態がOFFであろうがONであろうが、「通常の幼女たち22人全員が確実に最低1回は石像をOFFからONに切り替えた」と決定づける方法とは?
2回繰り返せばいいのです。
「通常の幼女たちが石像をOFFからONにする操作を2回まで行う」
「破壊役の幼女は、石像がONになっているのを確認した44回目で破壊する」
これならば石像の初期状態に左右されず、23人全員での解放が可能になります。
それぞれの場合を考えていきましょう。
石像の初期状態がOFFの場合
通常の幼女22人全員が2回ずつ石像をOFFからONに切り替えます。
これにより23人全員が石像の部屋に入ったことが確実になるため、幼女たちは解放されます。
石像の初期状態がONの場合
通常の幼女22人のうち、幼女21人が石像を2回ずつOFFからONに切り替えますが、残り1人(幼女X)は1回しか切り替えられません。
この場合、幼女Xが2回目の切替操作を行う前に破壊役幼女が石像を破壊します。
どの幼女も最低1回は石像の部屋に訪れているため、幼女たちは解放されます。
43回ではない
43回だと、確実な全員解放は不可能です。
石像の初期状態がONで、なおかつ通常の幼女たち22人のうち21人が2回ずつ石像のON/OFF切り替えを行なった場合、残り1人の通常の幼女が一度も石像の部屋に入らないまま石像が破壊される可能性があるからです。
最後に
ここまでお読みいただきありがとうございました。
この論理クイズが、激動の現代社会を駆け抜ける方々の清涼剤となりますように。
参考サイト
さまざまな論理パズルをでまとめていらっしゃるcatupperという方のGist(ソースコード共有サービス)です。
本論理クイズは、こちらの7番目のテキストファイル「7.23人の幼女と石像の館」から問題文の要旨を引用いたしました。
解答の参考にさせていただきました。
超難問論理クイズ「2人の幼女とチェス盤の部屋」が本当に難しすぎた
全く関係ないのですが、論理クイズとしては最難関レベルの問題です。
140字以内の問題文
23人の幼女が館に閉じ込められた。石像は東西南北のいずれかを向いている。幼女は1人ずつランダムに石像の部屋に呼ばれ、石像を「左に90度回転」「右に90度回転」「壊す」のいずれかの行動を取る。石像が壊れるとそれまで石像の部屋を訪れた幼女が全員解放される。全員が確実に解放されるには?