今回のテーマは「条件つき確率」。
簡単そうに見える問題でも、「条件」がつくと突然むずかしくなってしまう。
多くの人が頭を抱えたクイズをお楽しみください。
問題
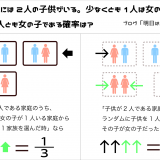
スミスさんには子供が2人いる。
1人は火曜日に生まれた女の子です。
では、2人とも女の子である確率は?
※男女が生まれる確率はそれぞれ50%とする
さあ、解いてみよう!
ノーヒントで。
少し下にスクロールすると答えがあります。
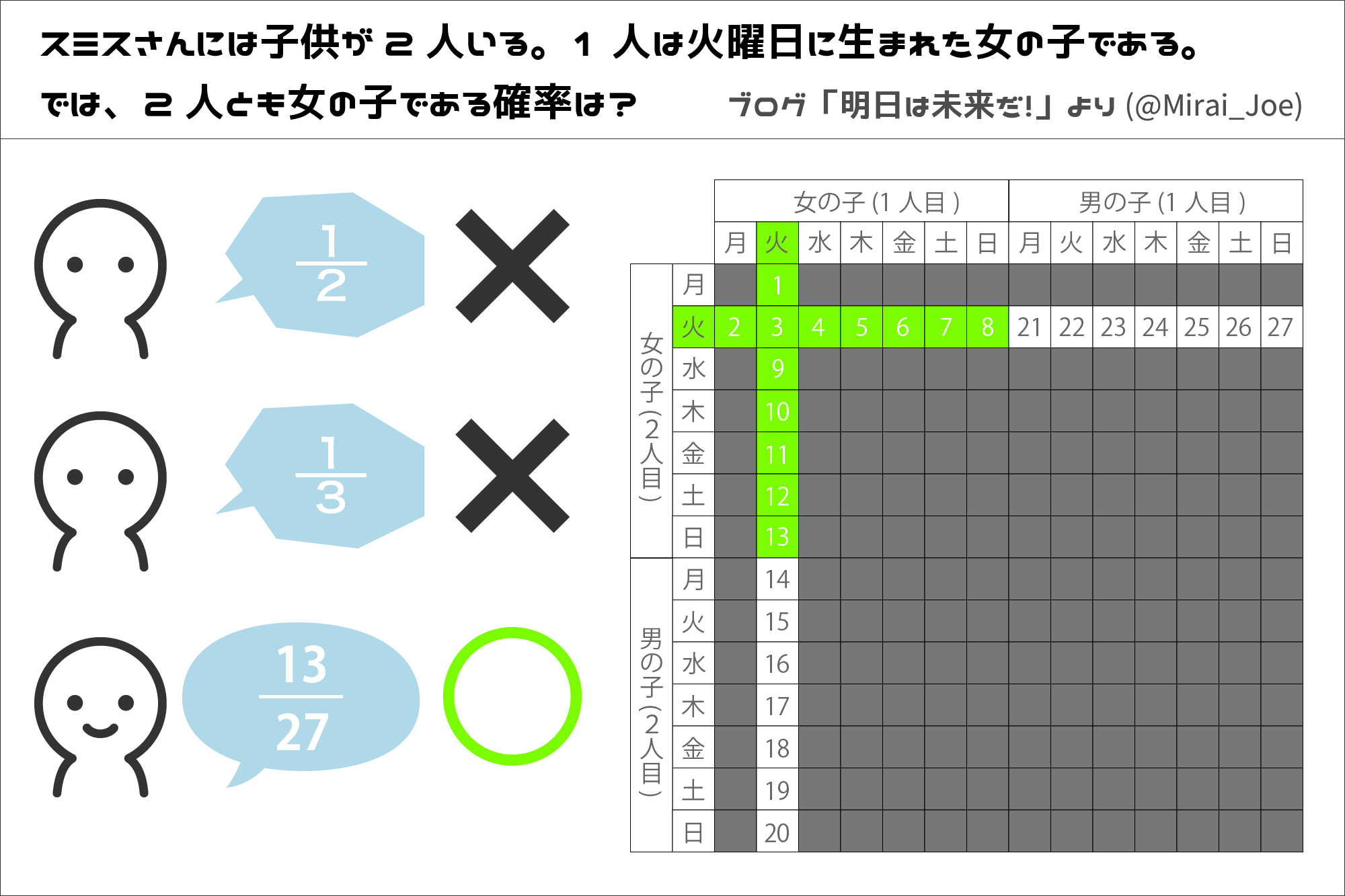
正解
13/27(48.1%)
解説
概要
本問は、2010年にアメリカ・シアトルで行われた講演会でゲイリー・フォシー(Gary Foshee)が出題した問題「火曜日に生まれた男の子」を元にしています。
この問題を初めて見た人は、おそらくこう思うことでしょう。
「生まれた曜日なんて関係あるのか?」
結論から言うと、大きく関係します。
問題文の「火曜日に生まれた男の子」を単に「男の子」と置き換えた場合、その結果は全く違うものになります。
いったい何が起こっているのか。
「13/27」という理解不能な数字はどこから出てきたのか。
さあ、確率の面白さをめぐる旅に出かけましょう。
解き方
上記の図をご覧ください。
1人目の子(年上)が火曜日生まれの女の子であるパターンは、(女,女)の7通りと(女,男)の7通り。
計14パターン。
2人目の子(年下)が火曜日生まれの女の子であるパターンは、(女,女)の7通りと(男,女)の7通り。
計14パターン。
ありえる組み合わせは28通り。
そのうち「少なくとも1人は火曜日生まれの女の子」である組み合わせは14通り。
ならば
14 / 28 = 1/2
が答えなのではないか? と思うかもしれません。
違います。
図の表の「3」と書かれた部分を見てください。
ここだけは「1人目が火曜の女の子のパターン」と「2人目が火曜の女の子のパターン」を数える時で、重複して2回数えています。
つまり、(火曜日の女の子,火曜日の女の子)のパターンだけ1つ少なく数えなければいけません。
ということは。
ありえる組み合わせは28通り
↓
ありえる組み合わせは27通り
「少なくとも1人は火曜日生まれの女の子」である組み合わせは14通り
↓
「少なくとも1人は火曜日生まれの女の子」である組み合わせは13通り
以上より、13/27 が正解になります。
問題文の意味
問題文の意味するところが、
「年上の子が火曜日に生まれた」
ではなく、
「少なくとも1人(あるいは2人とも)、火曜日に生まれた女の子がいる」
「そしてその女の子が”どちらの子”なのかは言いません」
であることに注意してください。
「特定の1人が火曜日生まれであるとき、特定のもう1人が女の子である確率」は1/2です。
この場合、「特定の1人が火曜日生まれであること」は「特定のもう1人が女の子であるかどうか」とは全く関係がありません。
「テイラー・スウィフトさんが火曜日生まれである時、アイリスフィールさんが女の子である確率は?」という質問と本質的には一緒です。(答えはもちろん1/2)
しかし、「2人いるうち、不特定の1人(あるいは2人とも)が火曜日生まれである時の、不特定のもう1人が女の子である確率」になると話は違います。
この確率が13/27になってしまうのは、「火曜日生まれの女の子がいる」という極めて重大な事象が全体に影響を与えてくるからです。
条件によって変わる確率
もし問題文が
スミスさんには子供が2人いる。
少なくとも1人は女の子です。
では、2人とも女の子である確率は?
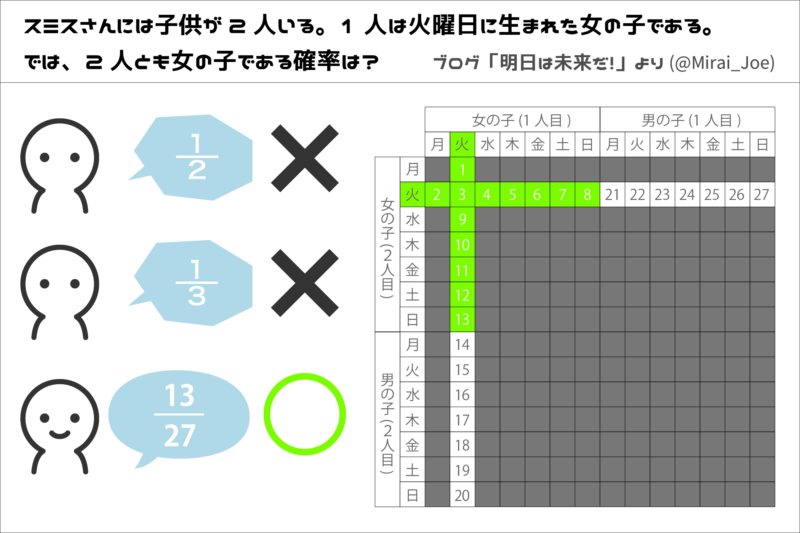
だった場合、確率は1/3(約33.3%)になります。
参考:「スミスさんの子供(2人の子供の性別問題)」
スミスさんには子供が2人いる。
少なくとも1人は火曜日に生まれた女の子です。
では、2人とも女の子である確率は?
の時(本問の場合)は13/27(約48.1%)
スミスさんには子供が2人いる。
少なくとも1人は火曜日の午前中に生まれた女の子です。
では、2人とも女の子である確率は?
の時は27/55(約49.0%)
下のイラストでなんとなくイメージをつかんでください。
とすると、当然出てくるのは次の疑問。
なぜ、「少なくとも1人は火曜日生まれである」という問題には何の関係もなさそうな条件によって「2人とも女の子である確率」が違ってきてしまうのか?
条件付き確率の世界へ
「少なくとも女の子が1人いる」
だった文から
「少なくとも火曜日生まれの女の子が1人いる」
という情報が増えたことで、何が起こったか?
なぜ確率は上昇したのか?
さあ、もう一度上のイラストを見てください!
白いマスは「問題の前提としてありえるパターン」。
「少なくとも1人の〜」という条件を満たすパターンです。
緑のマスは「正解としてありえるパターン」。
条件を満たした上で「2人とも女の子」を満たすパターンです。
確率 = それが起こる場合の数 / (条件を満たす)すべての場合の数
なので
正解 = 緑のマス / (緑のマス + 白いマス)
になります。
さて。
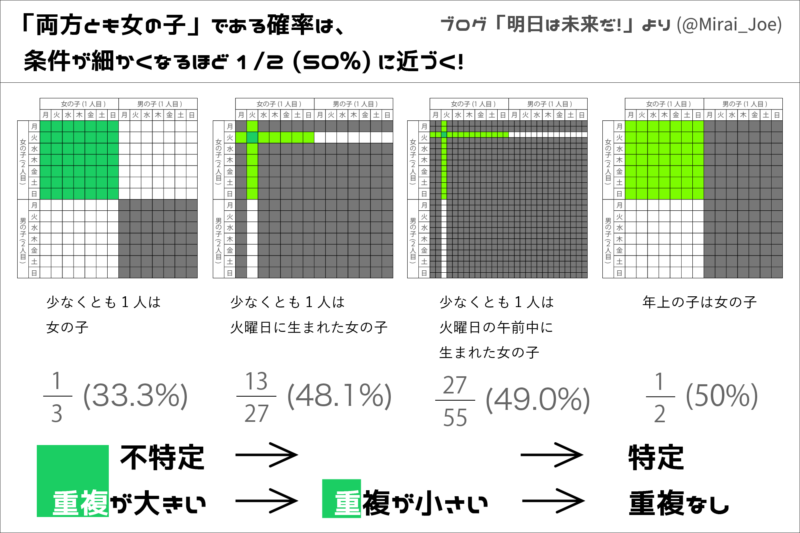
「1/3」の表と、「13/27」の表を見比べてください。
黒く塗りつぶされたマスが増えていますね。
「黒く塗りつぶされたマス」は、「可能性が排除されたパターン」です。
「男・男」は正解になりえませんからオールブラックになっています。
「少なくとも1人は女の子がいるパターン」
※緑のマス+白いマス「女・女」:49マス
「女・男」:49マス
「男・女」:49マス
「少なくとも1人は女の子がいて、2人とも女の子であるパターン」
※緑のマス「女・女」:49マス
「女・男」:0マス
「男・女」:0マス
ここまではいいですね。
それではいよいよ今日のハイライトに突入します。
「少なくとも1人は火曜日生まれの女の子がいるパターン」
※緑のマス+白いマス「女・女」:13マス
「女・男」:7マス
「男・女」:7マス
「少なくとも1人は火曜日生まれの女の子がいて、2人とも女の子であるパターン」
※緑のマス「女・女」:13マス
「女・男」:0マス
「男・女」:0マス
はいストップ!!
「少なくとも1人は女の子がいるパターン」
「少なくとも1人は火曜日生まれの女の子がいるパターン」
をもういちど比較してみましょう!
「少なくとも1人は女の子がいるパターン」
※緑のマス+白いマス「女・女」:49マス
「女・男」:49マス
「男・女」:49マス
「少なくとも1人は火曜日生まれの女の子がいるパターン」
※緑のマス+白いマス「女・女」:13マス (36マス減)
「女・男」:7マス (42マス減)
「男・女」:7マス (42マス減)
ここ!!
これです!!!
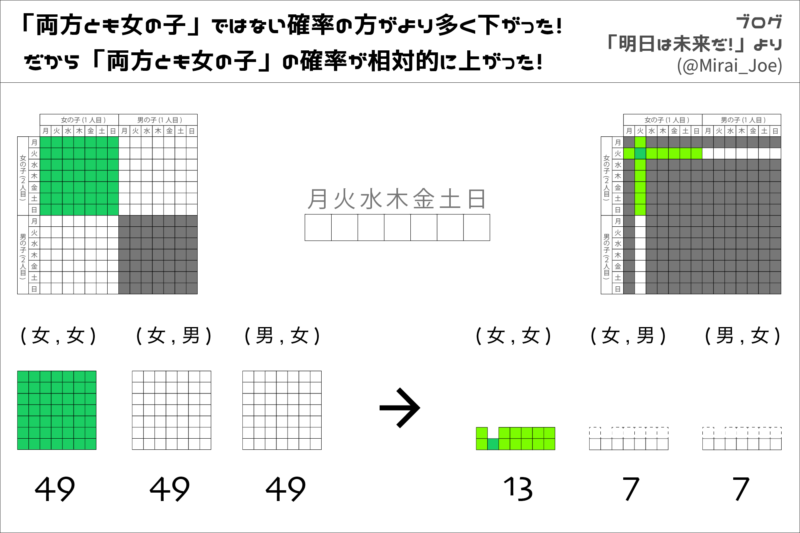
「火曜日生まれ」という条件が追加されたことで、
「2人とも女の子」ではないパターンの方がより多く減少しています。
その減少差はそれぞれ6マス。
火曜日を除いた6曜日の数と一致します!
そうです!
これが条件付き確率です!!!
条件が付けば、「正解となるパターンはしぼられる」……。
しかしそれ以上に、「不正解となるパターンの方が多くしぼられる」!!!
だから確率は上昇したのです!!
「2人とも女の子である確率」が上がった、
と言うより、
「2人とも女の子”ではない”確率」がより多く下がった!!
だから、相対的に「2人とも女の子である確率」が上昇したのです!!!!!
まとめ
あああああああああああああああああああ
確率って面白いなああああああああああああああああああああああ
ここまでお読みいただきありがとうございました!!!!!
この数学クイズが、明日を切り開き未来を追いかける方々の希望となりますように!!!!!!
うおおおおおおおおおおおおおおおおおおおおテンション上がってきたぜええええええええええええ
参考
Magic numbers: A meeting of mathemagical tricksters
Tuesday Changes Everything (a Mathematical Puzzle)
Tuesday’s child is full of probability puzzles
数学クイズ「スミスさんの子供(2人の子供の性別問題)」が世界一面白い
140字以内の問題文
スミスさんには子供が2人いる!!!
1人は火曜日に生まれた女の子だ!!!
では、2人とも女の子である確率は!!!???
※男女が生まれる確率はそれぞれ50%とするんだぜえええええええ