とても簡単なはずなのに、なぜか難しい。
今回ご紹介する数学クイズは超有名問題「スミスさんの子供」。
海外では「Boy or Girl paradox(2人の子供の性別問題)」として知られ、古くから大論争を巻き起こしてきた問題です。
日本では、登場人物を双子に置き換えた「双子の確率」「双子の性別問題」とも呼ばれています。
「確率」のややこしさを味わってください。
問題
スミスさんには2人の子供がいる。
少なくとも1人は女の子である。
では、2人とも女の子である確率は?
※男女が生まれる確率はどちらも50%とする
さあ、解いてみよう!
ヒントはなし。
見た目はシンプルですが、相当ややこしい話になります。
少し下にスクロールすると答えがあります。
正解
1/3 (約33%)
※ただし場合によっては1/2 (50%)
解説
本問の原型は、マーティン・ガードナー(Martin Gardner)が1959年に発表した「2人の子供の問題」です。
この問題の解釈を巡って、当時は議論が絶えませんでした。(今でもたまに話題になります)
現在では、公式的に決着がついています。
それでは解説を見ていきましょう。
前提
2人の子供の性別は(女,女)(女,男)(男,女)(男,男)という4通りの組み合わせが存在する。
| 年上 | 年下 | |
| パターン1 | 女の子 | 女の子 |
| パターン2 | 女の子 | 男の子 |
| パターン3 | 男の子 | 女の子 |
| パターン4 | 男の子 | 男の子 |
確率の謎
このクイズの難しさは「問題文の解釈により答えが2つ存在しうる」ところにあります。
問題となるのは「少なくとも1人は女の子である」という一文。
この問題を考える際、多くの人は次の3つの確率を混同します。
- 特定の1人が女の子だと分かった時、もう1人が女の子である確率(=1/2)
- 少なくとも1人が女の子だと分かった時、2人とも女の子である確率(=1/3)
- 不特定の1人が女の子だと分かった時、もう1人が女の子である確率(=1/2)
この問題の答えとして正しい「確率」は、2番目あるいは3番目の確率です。
それでは1つずつ確認していきましょう。
1. 特定の1人が女の子だと分かった時、もう1人が女の子である確率(=1/2)
「2人の子供。
1人は女の子。
ならばもう1人が女の子かどうかは、“既に性別が確定している1人の女の子”と何の関係もない。
だからもう1人が女の子である確率は50%だ」
この解釈は間違いです。
※ただし厳密に言うと「3番目の確率」における考え方とものすごく近いので、あながち大外れでもありません
もしも問題が、
Aさんには2人の子供がいる。
年上の子は女の子である。
2人とも女の子である確率は?
であったなら、何の問題もなく1/2(50%)が答えです。
確認してみましょう。
| 年上 | 年下 | |
| パターン1 | 女の子 | 女の子 |
| パターン2 | 女の子 | 男の子 |
| パターン3 | 男の子 | 女の子 |
| パターン4 | 男の子 | 男の子 |
年上の子が女の子である組み合わせは、(女,女)(女,男)の2通り。
そのうち2人とも女の子である組み合わせは、(女,女)の1通り。
よって1/2(50%)が正解です。
しかし「スミスさんの子供」では、「少なくとも1人は女の子がいる」としか言っていません。
つまり、元々の可能性にパターン3の(男,女)も加えなければならないのです。
この「1番目の確率」の考え方は、問題文を「特定の1人が女の子である」と誤認してしまうことによって起こる発想です。
2. 少なくとも1人が女の子だと分かった時、2人とも女の子である確率(=1/3)
それではいよいよ本題です。
前提となる「少なくとも1人は女の子」である組み合わせは(女,女)(女,男)(男,女)の3通り。
そして「2人とも女の子」である組み合わせは(女,女)の1通り。
| 年上 | 年下 | |
| パターン1 | 女の子 | 女の子 |
| パターン2 | 女の子 | 男の子 |
| パターン3 | 男の子 | 女の子 |
| パターン4 | 男の子 | 男の子 |
よって正解は「1/3」です。
この解釈では「少なくとも1人は女の子」をきわめて文字通りに、数学テスト的に、2人の子供がいる家庭を対象にして考えていることに着目してください。
このクイズにおいて最も一般的な「正答」であるとともに、最も多くの議論のマトになっている解釈です。
3. 不特定の1人が女の子だと分かった時、もう1人が女の子である確率(=1/2)
3番目の確率。
この解釈こそ当問題を難解せしめている筆頭です。
「少なくとも1人は女の子」。
では、「”その1人”とは誰のことを指しているのか?」
2人の子供の性別は(女,女)(女,男)(男,女)(男,男)という4通りの組み合わせが存在する。
(女,女)の姉の方。
(女,女)の妹の方。
(女,男)の姉の方。
(男,女)の妹の方。
ありえる家庭の組み合わせ——ではなく、「”少なくとも1人”の”1人”としてありえる組み合わせ」は4通り。
そのうち(女,女)となる組み合わせは2通り。
よって
2/4 = 1/2(50%)
が正解である。
| 年上 | 年下 | |
| パターン1 | 女の子 | 女の子 |
| パターン2 | 女の子 | 男の子 |
| パターン3 | 男の子 | 女の子 |
| パターン4 | 男の子 | 男の子 |
※表自体は「2番目の確率」のものと変わらない
本当の正解
2番目と3番目の確率の解釈は、いずれも理にかなっています。
いったいどちらが正解なのか。
基本的には2番目が正解。
が、想定されうる状況によっては3番目も正しい。
この混乱は、問題文のあいまいさが原因である。
が結論です。
当初、問題制作者マーティン・ガードナーは「1/3が正解である」としていました。
しかし問題文の解釈によっては(3番目の確率である)「1/2」も正解になりうると確認されたのです。
2つの解釈の大きな違い。
それは「少なくとも1人は女の子」という一文。
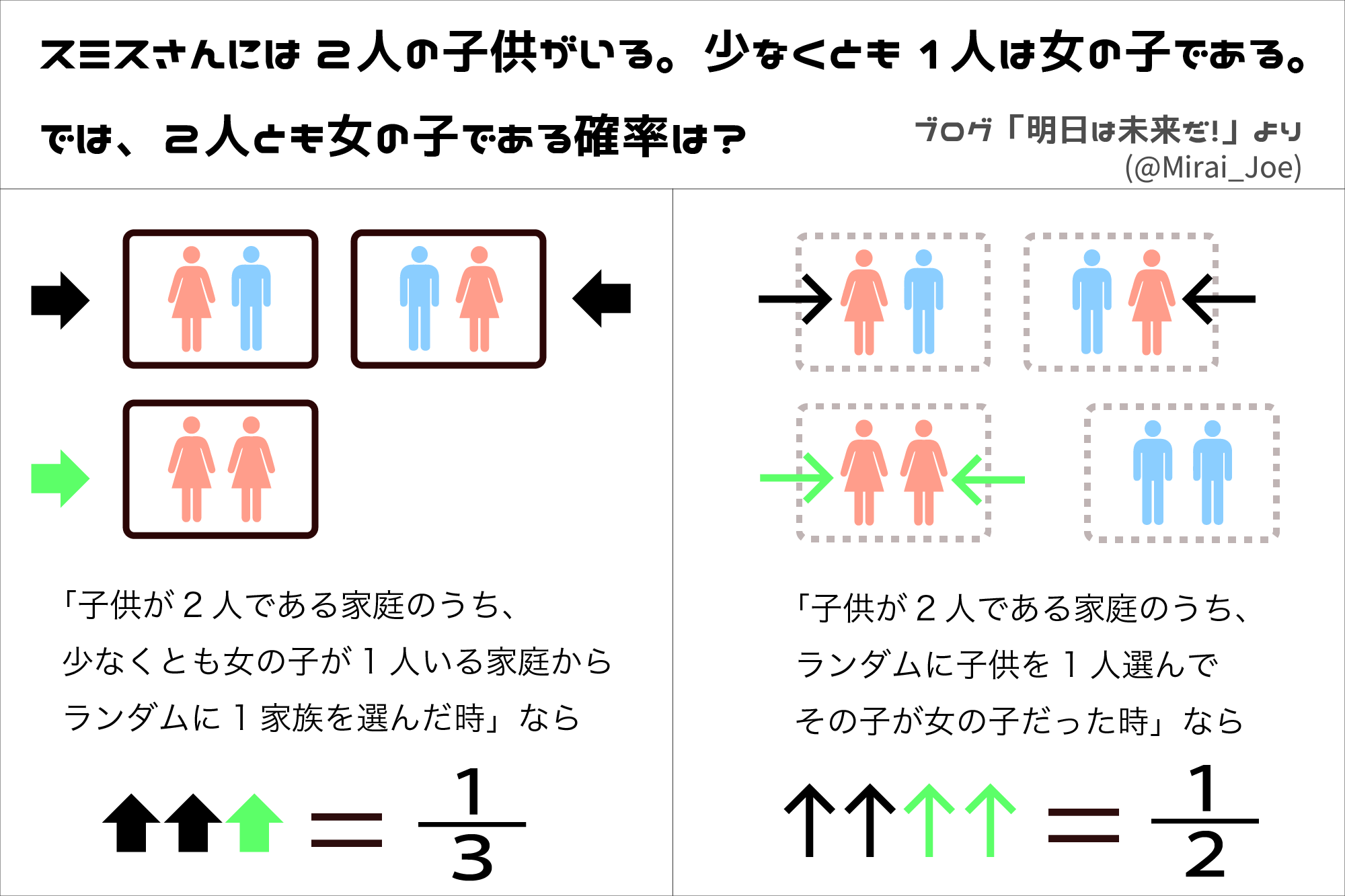
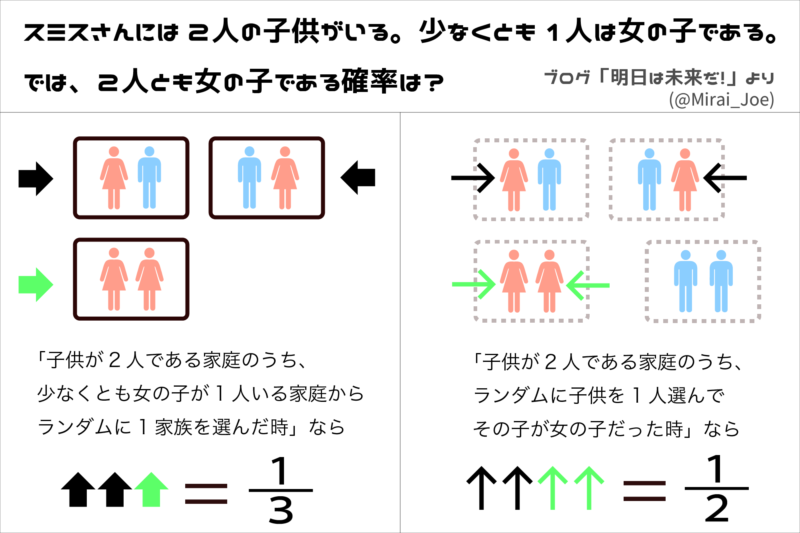
「2人の子供がいる家庭のうち、女の子が少なくとも1人いる家庭の中から、ランダムに1軒を選んで、その家庭が女の子2人である確率」
なのか、
「2人の子供がいる家庭のうち、ランダムに1人を選んで、その子が女の子だった場合、もう1人が女の子である確率」
なのかで判断が分かれたのです。
前者なら1/3、後者なら1/2が答えです。
「少なくとも1人は女の子」という事実が、どういう経緯で得られたのかという「事前情報の入手方法」によって、全く同じ文章でも完全に異なる答えになってしまう。
それがこの問題のキーポイントです。
実際、
スミスさんには2人の子供がいる。
「ひな祭りをする」と言っていた。
スミスさんの子が2人とも女の子である確率は?
スミスさんには2人の子供がいる。
道を歩いていたら娘さんを1人連れたスミスさんに会った。
スミスさんの子が2人とも女の子である確率は?
という2題ではそれぞれ答えが異なります。
(前者は1/3、後者は1/2)
今日では「スミスさんの子供」(2人の子供の性別問題)は、確率の難しさを象徴する例題として広く知られています。
図解/イラスト
まとめ
ここまでお読みいただきありがとうございました。
この数学クイズが、明日をつくる未来の担い手の方々の手助けとなりますように。
参考
140字以内の問題文
スミスさんには2人の子供がいる。
少なくとも1人は女の子である。
では、2人とも女の子である確率は?
※男女が生まれる確率はどちらも50%とする