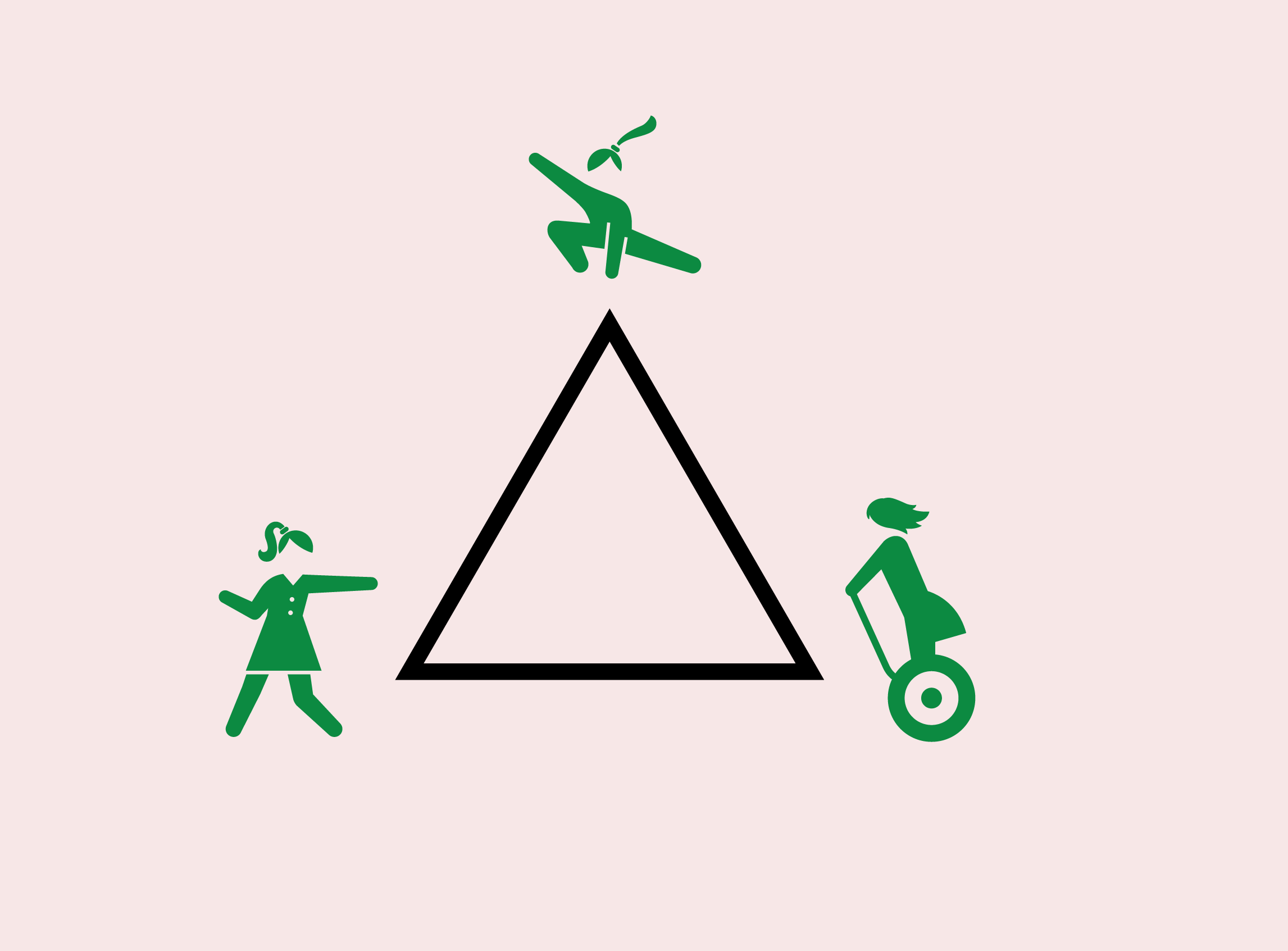数学クイズ「三角形でぶつかる少女」の答えが意外と簡単

問題

3人の少女が三角形の各頂点に立っている。

これから少女たちはランダムに方向を選び、三角形の辺に沿って「点」から「点」へ同時に移動を開始する。

移動が1回行われる時、2人の少女が衝突する確率はどのくらいだろうか？

三角形の頂点に1人ずつ。

全員がいっせいに別の頂点へと移動を開始した時、途中ではちあわせてしまう確率……。

なるほど。

可能性が多すぎてよく分からない。

––ように思えますが、考え方をすこし変えると驚くほど簡単に答えが出ます。

ヒントはなし。

少し下にスクロールすると答えがあります。

衝突する確率は75%

「3人のうち2人の少女が衝突する確率」をいきなり求めるのは難しそうです。

困った時の確率でおなじみの余事象を使いましょう。

雨が降らない確率 = 1 – 雨が降る確率

っていうアレです。

本問に置き換えると以下のようになります。

少女が衝突する確率 = 1 – 少女が衝突しない確率

それではさっそく「少女が誰も衝突しない確率」を求めていきましょう！

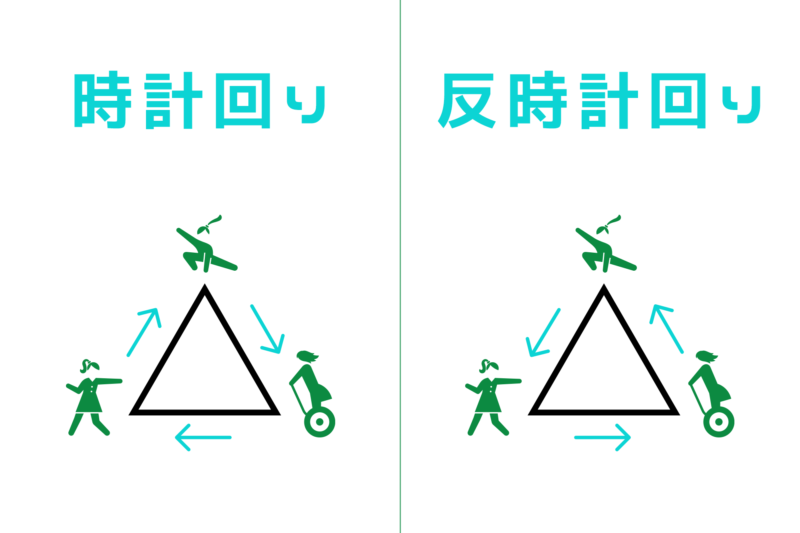
3人の少女はそれぞれ「時計回り」「反時計回り」のいずれかの方向をランダムに選んで進みます。
つまり、起こりうるすべての場合の数は2³ = 8通り

「少女が誰も衝突しない」という状況は

のいずれかが発生した時のみに起こります。

つまり、「衝突しない」という場合の数は2通り

以上より、

少女が衝突しない確率 = \( \frac{2}{8} = \frac{1}{4} \)

少女が衝突する確率 = 1 – 少女が衝突しない確率

少女が衝突する確率 = \( 1 – \frac{1}{4} = \frac{3}{4} \)

となり、少女は4分の3の確率（75%）で衝突します。

一見すると難しそうでも、視点を変えると一気に解きやすくなる––。

多くの数学問題に対して同じことが言えます。

困ったら着眼点を変更してみましょう。